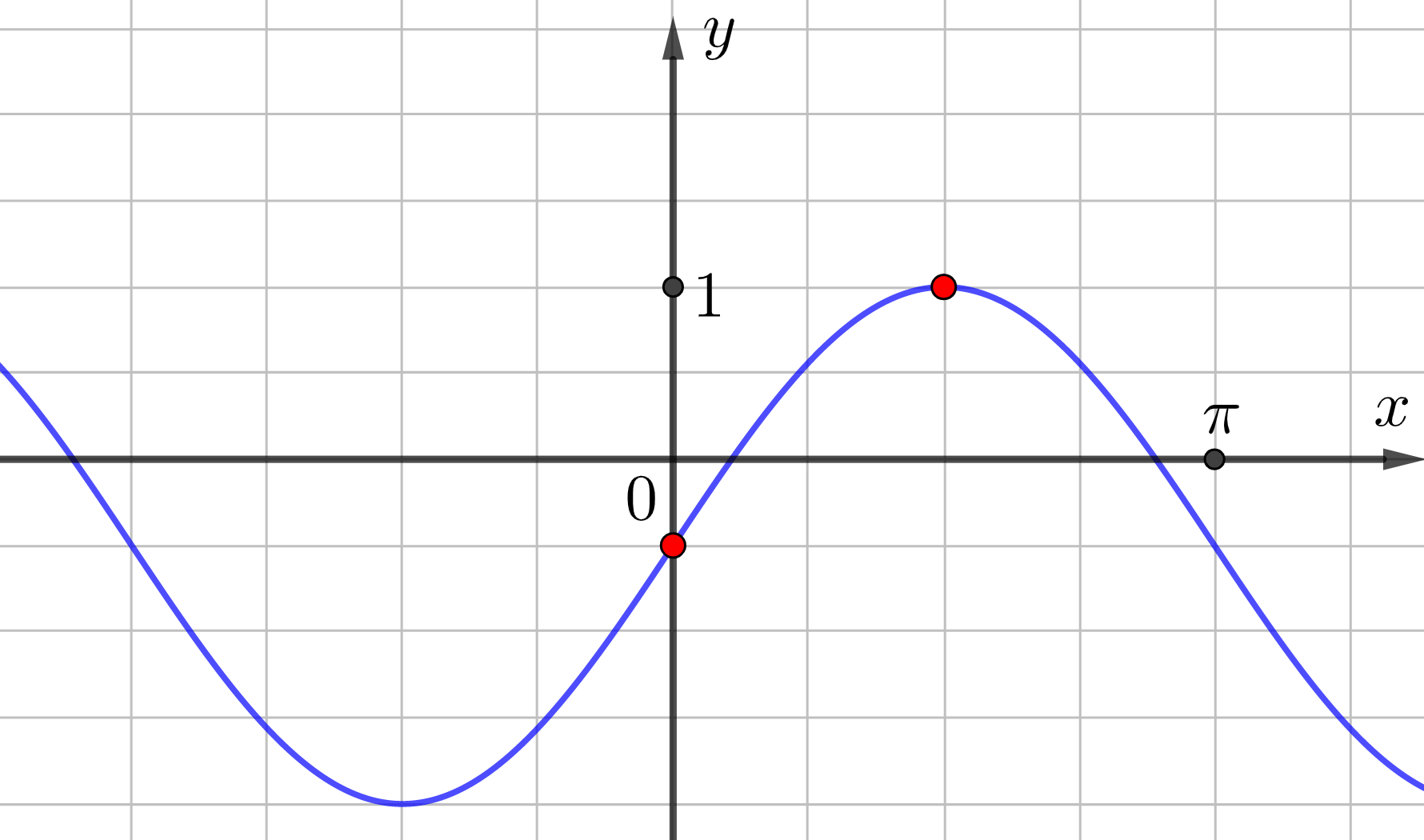
На рисунке изображён график функции \(\displaystyle f\left(x\right)=a\sin x +b{\small.}\) Найдите \(\displaystyle f\bigg(\frac{\pi}{6}\bigg){\small.}\)
\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\)
Чтобы найти \(\displaystyle f\bigg(\frac{\pi}{6}\bigg){\small,}\) найдём сначала неизвестные коэффициенты \(\displaystyle a\) и \(\displaystyle b{\small.}\)
Для этого составим систему уравнений относительно \(\displaystyle a\) и \(\displaystyle b\) и решим её.
Заметим, что точки, отмеченные на графике функции \(\displaystyle f(x)=a\sin x +b{ \small ,}\)
имеют координаты \(\displaystyle \Big(\color{blue}{0};\color{blue}{-\frac{1}{2}}\Big)\) и \(\displaystyle \Big(\color{green}{\frac{\pi}{2}};\color{green}{1}\Big){\small .}\)
Значит,
- при подстановке координат \(\displaystyle x=\color{blue}{0}\) и \(\displaystyle y=\color{blue}{-\frac{1}{2}}\) в уравнение \(\displaystyle y=a\sin x +b\) получим верное равенство;
- при подстановке координат \(\displaystyle x=\color{green}{\frac{\pi}{2}}\) и \(\displaystyle y=\color{green}{1}\) в уравнение \(\displaystyle y=a\sin x +b\) получим верное равенство.
Таким образом, получаем систему уравнений:
\(\displaystyle \left\{\begin{aligned}\color{blue}{-\frac{1}{2}}&=a\cdot \sin \color{blue}{0}+b{ \small ,}\\\color{green}{1}&=a\cdot \sin\color{green}{\frac{\pi}{2}}+b{ \small .}\end{aligned}\right. \)
Подставим вместо \(\displaystyle \sin \color{blue}{0}\) и \(\displaystyle \sin\color{green}{\frac{\pi}{2}}\) их значения.
Подставляя, получаем:
\(\displaystyle \left\{\begin{aligned}{-\frac{1}{2}}&=a\cdot 0+b{ \small ,}\\{1}&=a\cdot1+b\end{aligned}\right. \)
или
\(\displaystyle \left\{\begin{aligned}{-\frac{1}{2}}&=b{ \small ,}\\{1}&=a+b{ \small .}\end{aligned}\right. \)
Решим полученную систему уравнений.
Тогда исходная функция имеет вид:
\(\displaystyle f(x)=\frac{3}{2}\sin x -\frac{1}{2}{ \small .}\)
Найдём \(\displaystyle f\bigg(\frac{\pi}{6}\bigg){ \small:}\)
\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\frac{3}{2}\cdot \sin \frac{\pi}{6} -\frac{1}{2}{ \small .}\)
Значение \(\displaystyle \sin \frac{\pi}{6} \)– табличное. Подставим его:
\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\frac{3}{2}\cdot \sin \frac{\pi}{6} -\frac{1}{2}= \frac{3}{2}\cdot \frac{1}{2} -\frac{1}{2}=\frac{3}{4}-\frac{2}{4}=\frac{1}{4}=0{,}25{\small.}\)
Ответ: \(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=0{,}25{\small.}\)