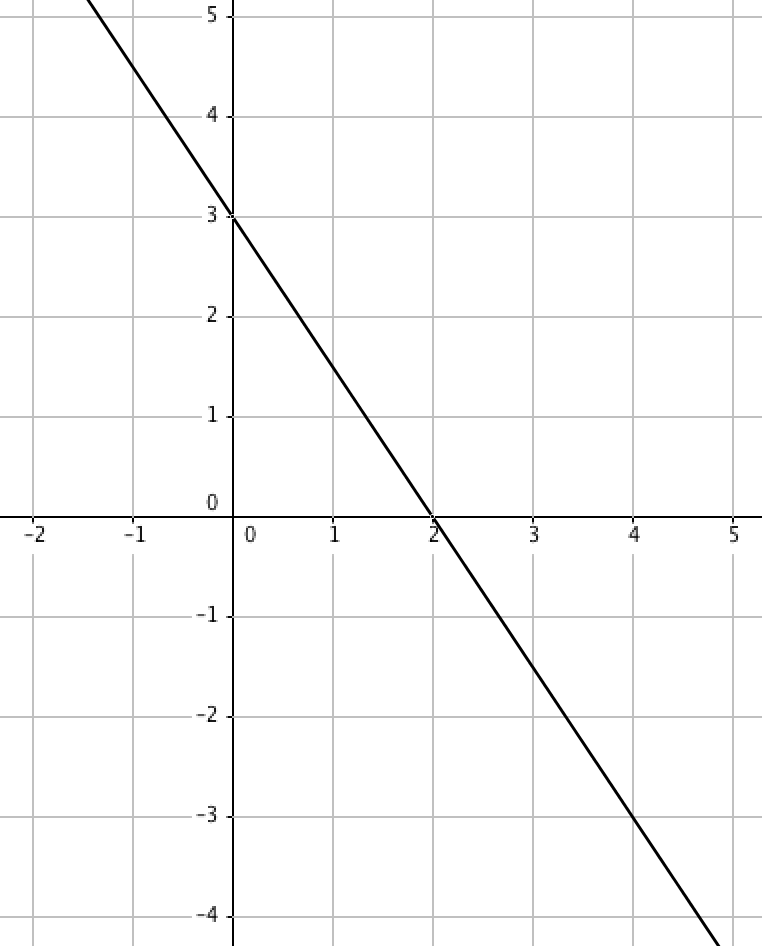
Түзу теңдеуді табыңыз:
\(\displaystyle y=\)
\(\displaystyle A\) және \(\displaystyle B\)нүктелерін түзу сызықта, ыңғайлы болу үшін, бүтін координаттармен таңдаңыз:
\(\displaystyle A(0;3)\) және \(\displaystyle B(2;0)\) нүктелерінің координаттарын \(\displaystyle y=kx+b\,{\small } \)түзу теңдеуіне ауыстырайық, .
\(\displaystyle A(\color{blue}{ 0};\color{green}{3}) \) нүктесінде \(\displaystyle x=\color{blue}{ 0}\) және \(\displaystyle y=\color{green}{ 3}{\small , }\) координаталары бар, сондықтан
\(\displaystyle \color{green}{3}=k\cdot \color{blue}{ 0}+b \)
немесе, дәл солай,
\(\displaystyle b=3{\small . }\)
\(\displaystyle B(\color{blue}{ 2};\color{green}{ 0}) \) нүктесінде \(\displaystyle x=\color{blue}{ 2}\) және \(\displaystyle y=\color{green}{ 0}{\small , }\) координаталары бар, сондықтан
\(\displaystyle \color{green}{ 0}=k\cdot \color{blue}{ 2}+b \)
немесе, дәл солай,
\(\displaystyle 2k+b=0{\small . } \)
Біз \(\displaystyle k \) және \(\displaystyle b, \) коэффициенттері үшін екі теңдеу алдық және теңдеулер жүйесін жаза аламыз:
\(\displaystyle \left\{\begin{aligned}b&=3{\small , }\\2k+b&=0{\small . }\end{aligned}\right.\)
Бұл жүйені шешеміз.
Осылайша, \(\displaystyle k=-\frac{ 3}{ 2}\) және \(\displaystyle b=3{\small} \)
\(\displaystyle k \) және \(\displaystyle b \) \(\displaystyle y=kx+b{\small , } \) үшін табылған мәндерді y=kx+b түзу теңдеуіне ауыстыра отырып, біз аламыз:
\(\displaystyle y=-\frac{ 3}{ 2}x+3{\small . } \)
Жауабы: \(\displaystyle y={\bf -\frac{ 3}{ 2}x+3}{\small . } \)