\(\displaystyle A(4;3)\) және \(\displaystyle B(4;\, 1){\small }\)нүктелері арқылы өтетін түзудің теңдеуін табыңыз:
\(\displaystyle x=\)
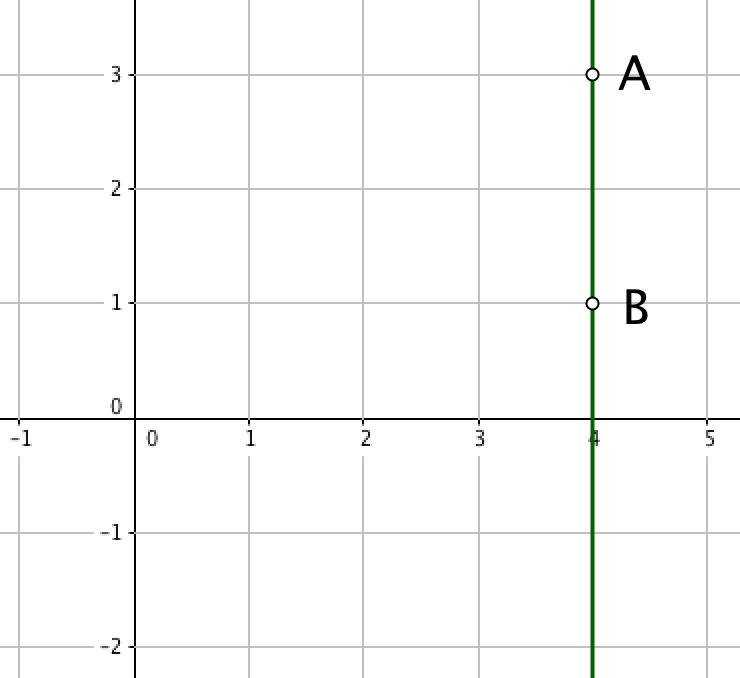
Түзу беріледі:
- немесе \(\displaystyle y=kx+b{\small ,}\) теңдеуі, кейбір \(\displaystyle k,\, b\) сандары үшін (яғни сызықтық функцияның графигі),
- немесе \(\displaystyle x=a{\small ,}\) теңдеуімен, кейбір \(\displaystyle a{\small .}\)саны үшін.
Есептегі графиктен берілген түзудің OY осіне параллель екендігі шығады, демек ол\(\displaystyle x=a {\small }\)теңдеуімен беріледі.
Бұл теңдеуді табу үшін түзу сызықтағы нүктелердің бірін алайық, мысалы, \(\displaystyle A(4;3){\small . }\)
Оның координаттарын түзудің \(\displaystyle x=a\,{\small } \)теңдеуіне ауыстырайық, .
\(\displaystyle A(\color{blue}{ 4};\color{green}{3}) \) нүктесі \(\displaystyle x=\color{blue}{ 4}\) және \(\displaystyle y=\color{green}{ 3}{\small , }\) координаталары бар , сондықтан
\(\displaystyle \color{blue}{ 4}=a {\small , }\)
немесе
\(\displaystyle a=4{\small . } \)
Осылайша, түзудің теңдеуі келесідей:
\(\displaystyle x=4{\small . } \)
Жауабы: \(\displaystyle x={\bf 4}{\small . } \)