Егер \(\displaystyle k>1{\small }\) белгілі болса, \(\displaystyle y=-kx^2{\small }\) квадраттық функциясының графигін таңдаңыз.
Егер \(\displaystyle \color{blue}{ k}>1{ \small }\) болса , онда нөлдік емес \(\displaystyle x_0\) үшін \(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) координаттары бар нүкте \(\displaystyle \color{green}{ (x_0; -x_0^2)}{ \small } \) координаттары бар нүктесінен төмен орналасқан, себебі \(\displaystyle \color{blue}{ -kx_0^2}<\color{green}{ -x_0^2}{\small .}\)
Осылайша, \(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) түрінің БАРЛЫҚ нүктелері (\(\displaystyle (0;0)\) нүктесінен басқа) \(\displaystyle \color{green}{ (x_0; -x_0^2)}{ \small } \) түрінің координаттары бар нүктелерден төмен орналасқан:
\(\displaystyle \color{blue}{ (x_0;\,-kx_0^2)} \) түрінің барлық нүктелері – бұл \(\displaystyle y=\color{blue}{ -kx^2}{\small }\) параболасы.
\(\displaystyle \color{green}{ (x_0; -x_0^2)}\) түрінің барлық нүктелері – бұл \(\displaystyle y=\color{green}{ -x^2}{\small }\) параболасы.
Демек, \(\displaystyle y=\color{blue}{ -kx^2}\) квадраттық функциясының графигі \(\displaystyle y=\color{green}{ -x^2}{\small }\) параболасынан төмен орналасқан:
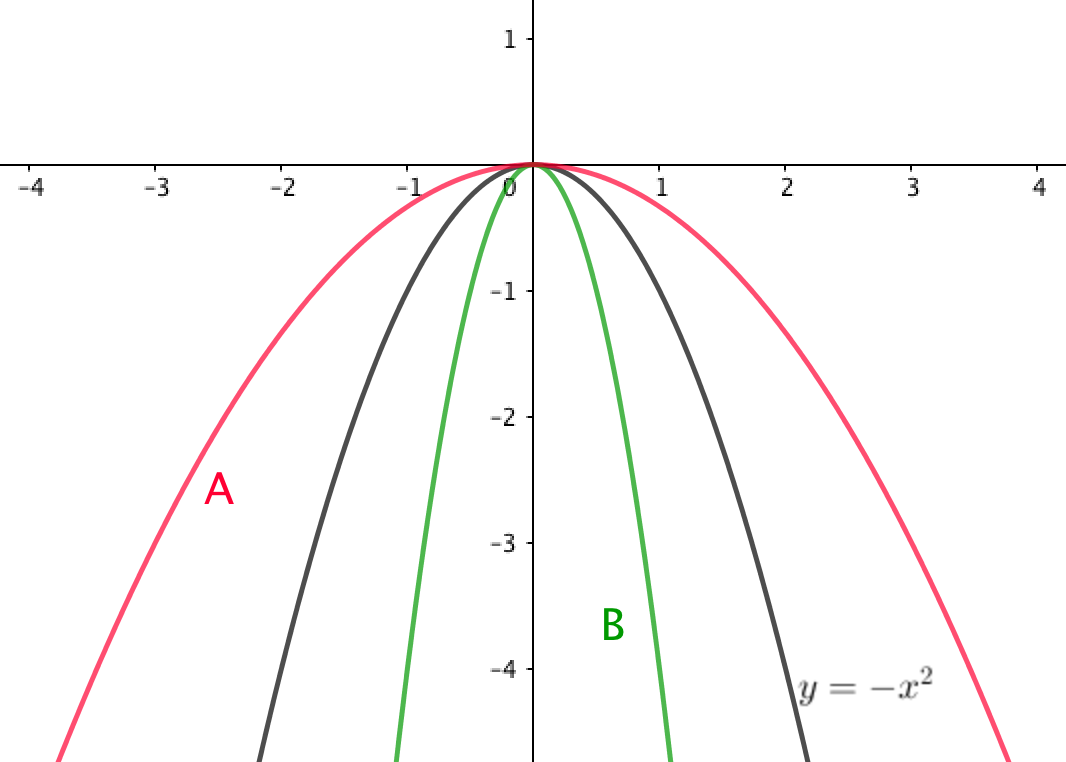
Шартта берілген суретті қарастырайық:

Бұл жағдайда \(\displaystyle y=-kx^2\) параболасының графигі \(\displaystyle y=-x^2{ \small } \) параболасының графигінен төмен болғандықтан, онда дұрыс жауап \(\displaystyle \color{green}{\rm B}{\small .} \)