\(\displaystyle y=-0{,}2x^2\) квадраттық функциясының графигі \(\displaystyle y=-x^2\) квадраттық функциясынан алынған
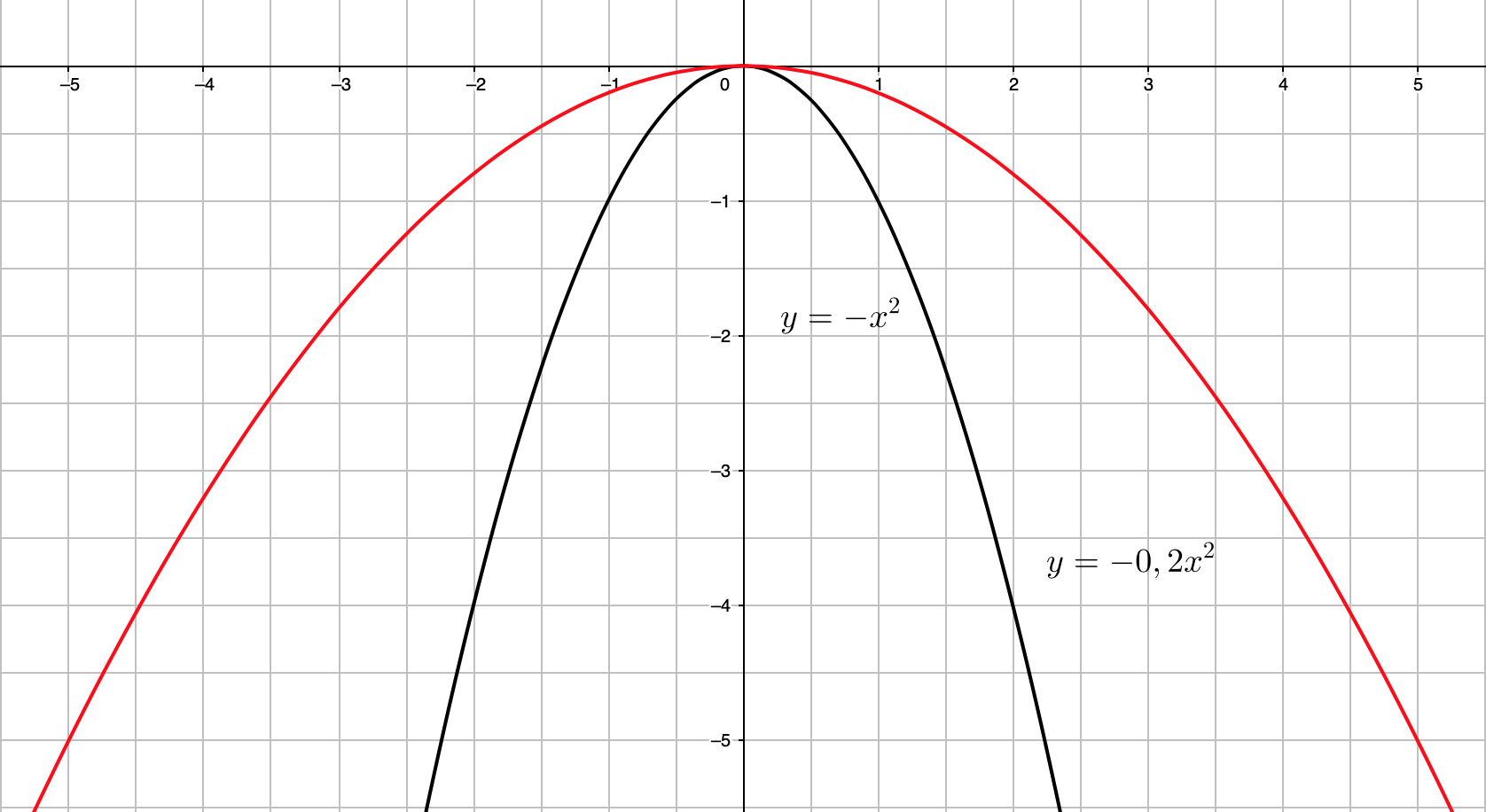
\(\displaystyle y=\color{blue}{ -x^2}\) параболасының графигі барлық нақты \(\displaystyle x{\small }\) сандары үшін \(\displaystyle \{(\color{blue}{ x};\, \color{blue}{ -x^2}) \}\) түрінің нүктелер жиыны болып табылады.
\(\displaystyle y=\color{red}{ -0{,}2x^2}\) параболасының графигі барлық нақты \(\displaystyle x{\small }\) сандары үшін \(\displaystyle \{(\color{red}{ x};\, \color{red}{ -0{,}2x^2}) \}\) түрінің нүктелер жиыны болып табылады.
\(\displaystyle y=-x^2 \) параболасының \(\displaystyle \rm OY \) осі бойымен \(\displaystyle k \) есе қысылуы - бұл графиктің барлық \(\displaystyle (x; -x^2) \) нүктелері үшін \(\displaystyle y \) координатасын \(\displaystyle k>1{\small }\) болғандағы \(\displaystyle k \) бөлу.
\(\displaystyle y=\color{blue}{-x^2} \) және \(\displaystyle y=\color{red}{-0{,}2x^2}{\small } \) параболалары үшін \(\displaystyle y \) координатасының қалай өзгергенін салыстырайық:
\(\displaystyle \color{blue}{-x^2}\longrightarrow\,\color{red}{-0{,}2x^2}= \color{red}{-\frac{2}{ 10 }x^2}= \color{red}{-\frac{x^2}{\phantom{1}\frac{ 10}{ 2 }\phantom{1}}}=\color{red}{ -\frac{ x^2}{ 5 }}\)
Яғни бұрын \(\displaystyle \color{blue}{ -x^2}{ \small } \) болған, және енді \(\displaystyle \color{red}{ -\frac{ x^2}{ 5 }}{\small } \) болды. Демек, \(\displaystyle y \) координатасы
\(\displaystyle \frac{\color{blue}{ -x^2}}{ \phantom{1}\color{red}{ -\frac{ x^2}{ 5 }}\phantom{1}}=5{\small } \) бөлінді
\(\displaystyle 5>1{ \small } \) бөлу орын алғандықтан, бұл \(\displaystyle y \) координатасы \(\displaystyle 5>1{ \small } \) бөлінгенін білдіреді.
Демек, \(\displaystyle y=-x^2 \) параболасының графигін \(\displaystyle \rm OY \) осі бойымен \(\displaystyle 5\) есе қысу орын алды.
Жауабы: \(\displaystyle y=-x^2 \) параболасының графигі \(\displaystyle \rm OY \) осі бойымен \(\displaystyle 5\) есе қысылған.