\(\displaystyle f(x)=\left(9-x\right)e^{x+9}{\small}\) функцияның ең үлкен нүктесін табыңыз
1) \\(\displaystyle f(x)=\left(9-x\right)e^{x+9}{\small}\) функциясының туындысын табыңыз.
Өрнекті \(\displaystyle -e^{x+9}+(9-x)e^{x+9}{\small}\) жеңілдету
Жақшаның ішінен \(\displaystyle e^{x+9}\) шығарайық, содан кейін ұқсас шарттарды берейік:
\(\displaystyle \begin{aligned}-e^{x+9}+(9-x)e^{x+9}=\left(-{\color{red}{\underline{\underline{\color{black}{1}}}}}+{\color{red}{\underline{\underline{\color{black}{9}}}}}-\color{red}{\underline{\color{black}{x}}}\right)e^{x+9}=\left({\color{red}{\underline{\underline{\color{black}{8}}}}}-\color{red}{\underline{\color{black}{x}}}\right)e^{x+9}{\small.}\end{aligned}\)
Осылайша, біз аламыз:
\(\displaystyle f^{\prime}(x)=-e^{x+9}+(9-x)e^{x+9}=\left(8-x\right)e^{x+9}{\small.}\)
2) \(\displaystyle f^{\prime}(x)=0{\small}\) болатын нүктелерді табайық.
\(\displaystyle f^{\prime}(x)=(8-x)e^{x+9}{\small}\) болғандықтан, ол үшін \(\displaystyle (8-x)e^{x+9}=0{\small}\) теңдеуін шешу керек.
3) Туындының түбірлерін нақты түзуде белгілейміз, сонымен қатар оның пайда болған интервалдардағы белгілерін анықтаймыз.
- \(\displaystyle \color{green}{(-\infty;\,8)}\) функциясы \(\displaystyle f^{\prime}(x)>0{\small}\) интервалында
- интервалында \(\displaystyle \textcolor{blue}{(8;\, +\infty)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small.}\)
Суреттегі туындының белгілерін белгілей отырып, біз аламыз:
4) Ережені пайдаланып \(\displaystyle f(x)=\left(9-x\right)e^{x+9}{\small}\) функцияның өсу және кему аралықтарын анықтайық.
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)>0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) өсуде \(\displaystyle \nearrow\)
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)<0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) кемуде \(\displaystyle \searrow\)
\(\displaystyle f'(x){\small}\) туындының белгілерін білу \(\displaystyle f(x){\small}\) өсу және кему аралықтарын анықтау:
Схемалық \(\displaystyle f(x){\small}\) түрде көрсетіңіз
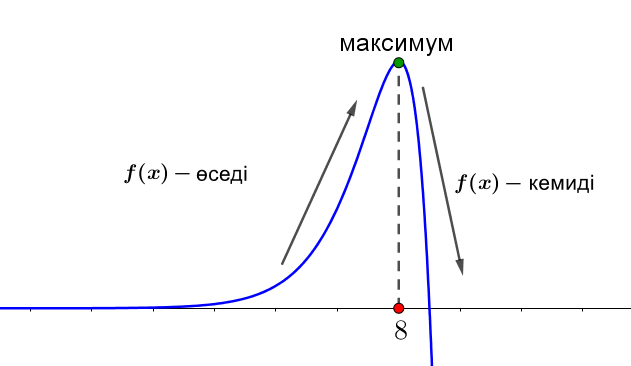
Демек, \(\displaystyle x=8\) - функцияның ең үлкен нүктесі \(\displaystyle f(x)=\left(9-x\right)e^{x+9}{\small.}\)
Жауабы: \(\displaystyle 8{\small.}\)