Өрнектің мәнін табыңыз:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\)
Берілген \(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}\) айырмасының ортақ көбейткіші \(\displaystyle \sqrt{3}{\small}\) бар. Оны жақшаның сыртына шығарамыз:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}}) {\small.}\)
Жақшада косинус пен синус квадраттарының айырмасы пайда болды.
Бұл жағдайда синус та, косинус та бірдей \(\displaystyle \frac{5\pi}{12}\) бұрышына ие.
Демек, қос бұрыштың косинус формуласын қолдануға болады:
\(\displaystyle \cos\, 2\color{red}{\alpha}=\cos^2\color{red}{\alpha}-\sin^2\color{red}{\alpha}\)
Біздің жағдайда \(\displaystyle \alpha=\frac{5\pi}{12},\) яғни
\(\displaystyle \cos^2 \color{red}{\frac{5\pi}{12}}-\sin^2 \color{red}{\frac{5\pi}{12}}=\cos(2 \cdot \color{red}{\frac{5\pi}{12}})\)
және \(\displaystyle 2 \cdot \frac{5\pi}{12}=\frac{5\pi}{6}\) болғандықтан, онда
\(\displaystyle \cos^2 \frac{5\pi}{12}-\sin^2 \frac{5\pi}{12}=\cos \frac{5\pi}{6}{\small.}\)
Сонда:
\(\displaystyle \sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}}) =\sqrt{3} \cos \frac{5\pi}{6} {\small.}\)
\(\displaystyle \cos \frac{5\pi}{6} {\small}\) неге тең екенін табамыз:
\(\displaystyle \frac{5\pi}{6}=\pi-\frac{\pi}{6}{\small .}\)
Сонда
\(\displaystyle \cos \frac{5\pi}{6} =\cos (\pi-\frac{\pi}{6}){\small .}\)
Ережеге сәйкес келтіру формуласын қолданамыз:
1) Бұрыш орналасқан ширекті анықтаймыз.
2) Бастапқы функцияның таңбасын анықтаймыз.
3) Қандай функция болатынын анықтаймыз.
Егер \(\displaystyle \pm \alpha \) бұрышына келесілерді қосып немесе азайтсақ
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (\(\displaystyle \pi\) бүтін саны), онда функцияны өзгертпейміз;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (\(\displaystyle \pi\) жартыларының тақ саны), онда функцияны өзгертеміз: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) және \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg\).
1. \(\displaystyle \pi-\frac{\pi}{6}{}\) бұрышы қай ширекте орналасқанын анықтаймыз:
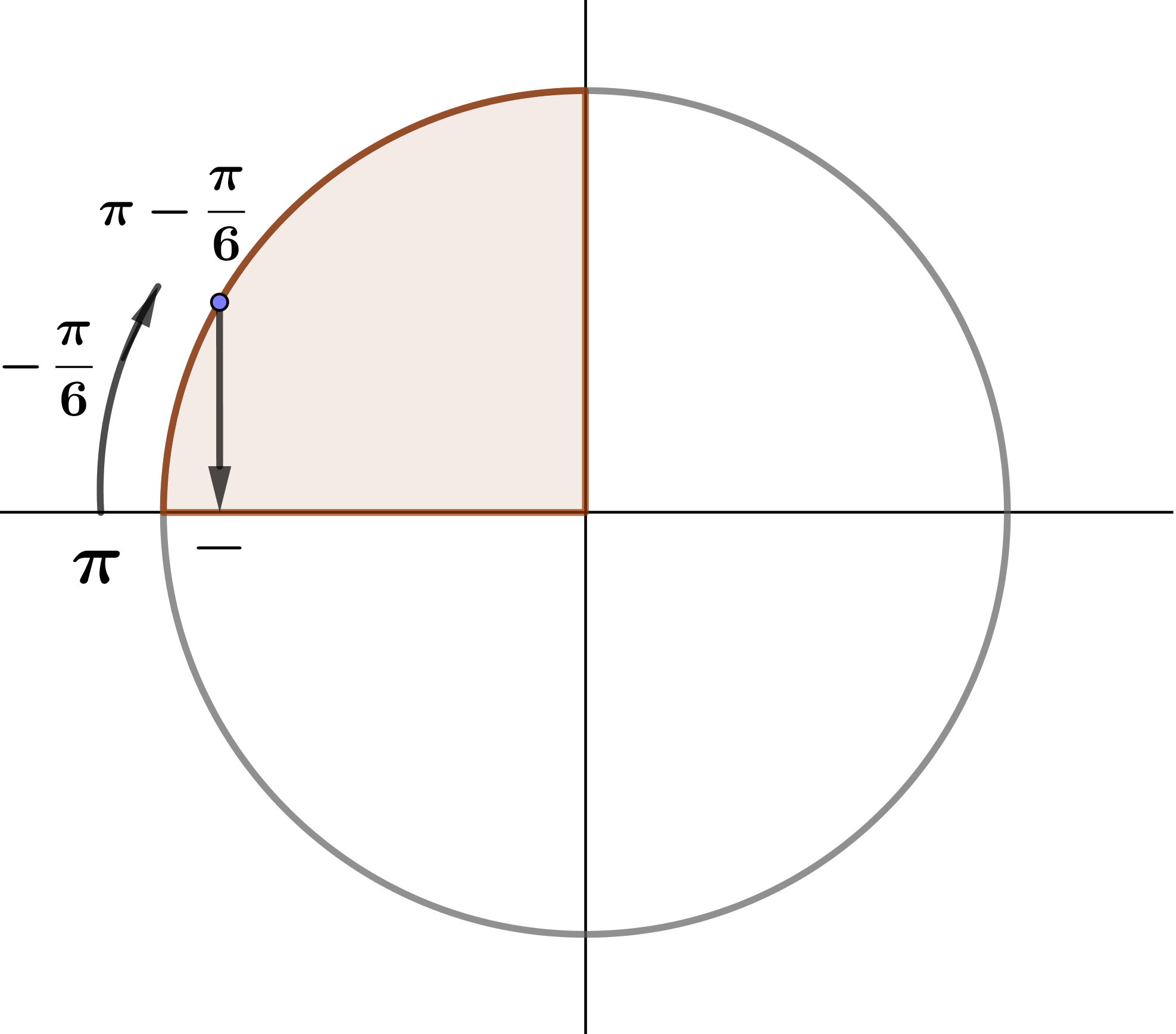
Демек, \(\displaystyle \pi-\frac{\pi}{6} \) бұрышы екінші ширекте орналасқан.
2. Бастапқы функцияның таңбасын анықтайық.
Екінші ширекте косинус теріс (\(\displaystyle {\bf -}\)).
3. Қандай функция болатынын анықтаймыз.
\(\displaystyle -\frac{\pi}{6}\) аргументіне \(\displaystyle \pi \) қосылатындықтан, функция өзгермейді.
Демек,
\(\displaystyle \cos {(\pi-\frac{\pi}{6})}=-\cos {\frac{\pi}{6}} {\small ,}\)
то есть \(\displaystyle \cos \frac{5\pi}{6}=-\cos {\frac{\pi}{6}} {\small .}\)
Сонда:
\(\displaystyle \sqrt{3} \cos \frac{5\pi}{6}=-\sqrt{3} \cos \frac{\pi}{6}{\small .}\)
Кестелік мәнді қоямыз.
\(\displaystyle - \sqrt{3} \cos \frac{\pi}{6}=-\sqrt{3} \cdot \frac{\sqrt{3}}{2}=-\frac{3}{2}=-1{,}5{\small.}\)
Осылайша, келесі теңдік тізбегі дұрыс:
\(\displaystyle \sqrt{3}\cos^2 {\frac{5\pi}{12}} -\sqrt{3} \sin^2 {\frac{5\pi}{12}}=\sqrt{3}\,(\cos^2 {\frac{5\pi}{12}} -\sin^2 {\frac{5\pi}{12}})=\sqrt{3} \cos \frac{5\pi}{6}=-\sqrt{3} \cos \frac{\pi}{6}=-\sqrt{3} \cdot \frac{\sqrt{3}}{2}=-1{,}5{\small.}\)
Жауабы: \(\displaystyle -1{,}5 {\small.} \)