Бұрыштардың арнайы мәндері үшін синус және косинус мәндері:
| Бұрыш | \(\displaystyle \sin\) | \(\displaystyle \cos\) |
| \(\displaystyle 0\) | \(\displaystyle \sin 0^\circ=0\) | \(\displaystyle \cos 0^\circ=1 \) |
| \(\displaystyle \frac{\pi}{2}\) | \(\displaystyle \sin\frac{\pi}{2}=1\) | \(\displaystyle \cos\frac{\pi}{2}=0 \) |
| \(\displaystyle \pi\) | \(\displaystyle \sin\pi=0\) | \(\displaystyle \cos\pi=-1 \) |
| \(\displaystyle \frac{3\pi}{2}\) | \(\displaystyle \sin\frac{3\pi}{2}=-1\) | \(\displaystyle \cos\frac{3\pi}{2}=0 \) |
Бірлік тригонометриялық шеңбердің қасиеті бойынша \(\displaystyle \alpha{ \small}\) шамасының орталық бұрышы беретін шеңбердегі нүкте \(\displaystyle (\cos\alpha;\, \sin\alpha){\small}\) координаталарына ие:
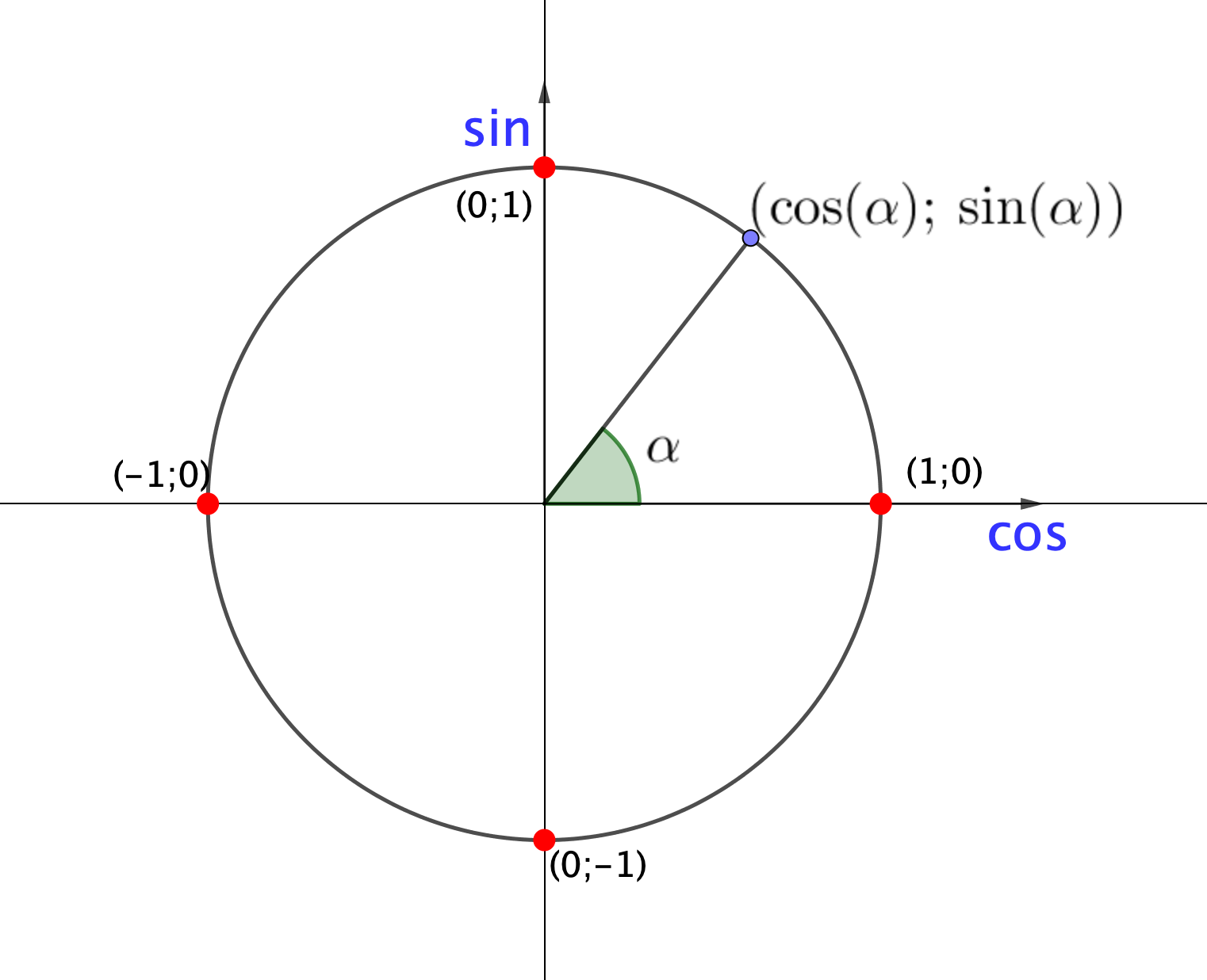
Сонда:
1) \(\displaystyle \bf 0{ \small}\) шамасының бұрышынан пайда болған нүкте \(\displaystyle (1;\, 0){\small}\) координаталарына ие. Демек,

\(\displaystyle \sin 0=0\) және \(\displaystyle \cos 0=1{\small .}\)
2) \(\displaystyle \bf \frac{\pi}{2}{ \small}\) шамасының бұрышынан пайда болған нүкте \(\displaystyle (0;\, 1){\small}\) координаталарына ие. Демек,

\(\displaystyle \sin\frac{\pi}{2}=1\) және \(\displaystyle \cos\frac{\pi}{2}=0{\small .}\)
3) \(\displaystyle \pi{ \small}\) шамасының бұрышынан пайда болған нүкте \(\displaystyle (-1;\, 0){\small}\) координаталарына ие. Демек,
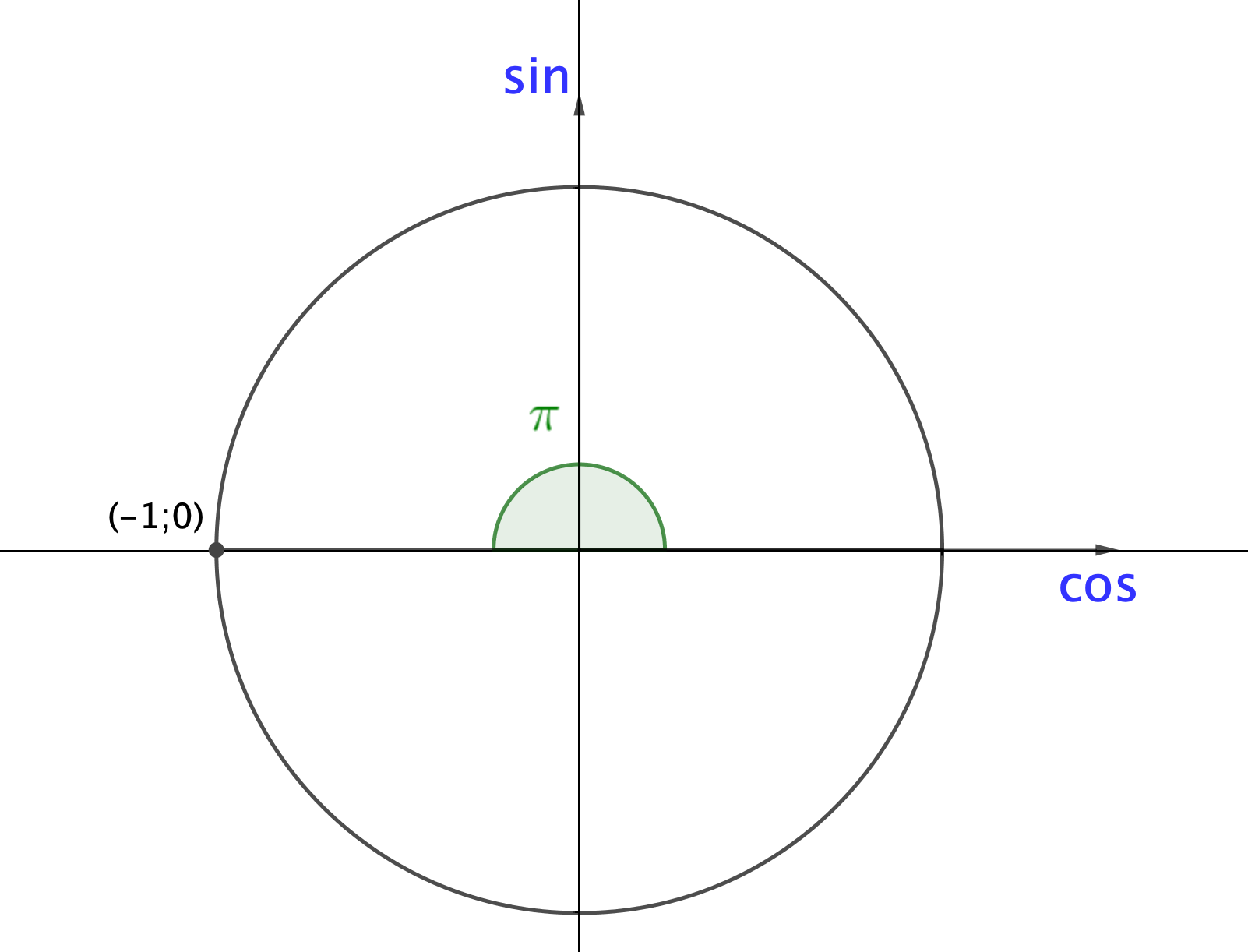
\(\displaystyle \sin\pi=0\) және \(\displaystyle \cos\pi=-1{\small .}\)
4) \(\displaystyle \bf \frac{3\pi}{2}{ \small}\) шамасының бұрышынан пайда болған нүкте \(\displaystyle (0;\, -1){\small}\) координаталарына ие. Демек,
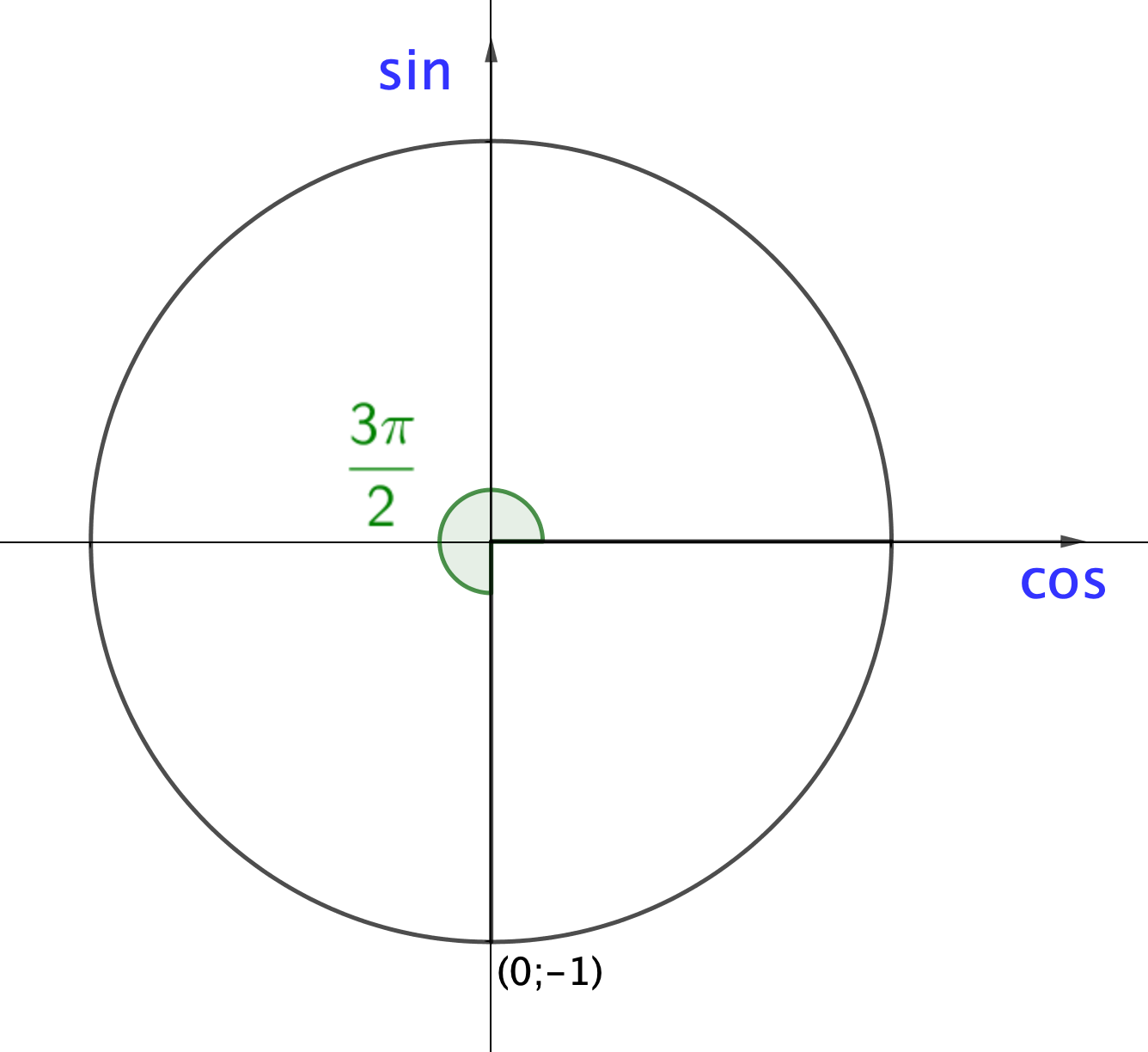
\(\displaystyle \sin\frac{3\pi}{2}=-1\) және \(\displaystyle \cos\frac{3\pi}{2}=0{\small .}\)