\(\displaystyle A\) нүктесін координаталары
\(\displaystyle (1{,}3;\, \sin(1{,}3)){\small}\) болатын нүктеге көшіріңіз.
Тексеру мәнін енгізіңіз:
\(\displaystyle \color{green}{M}=\)
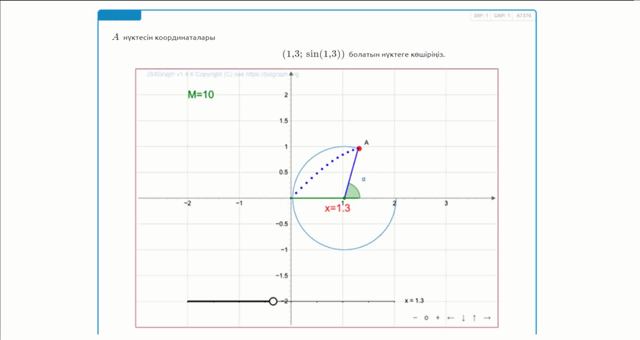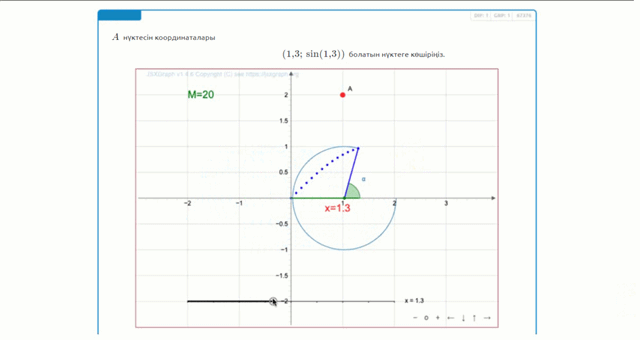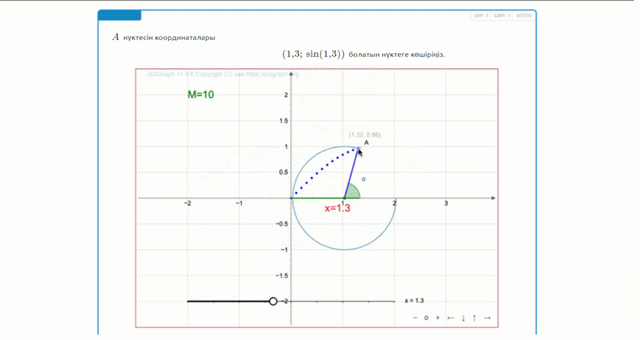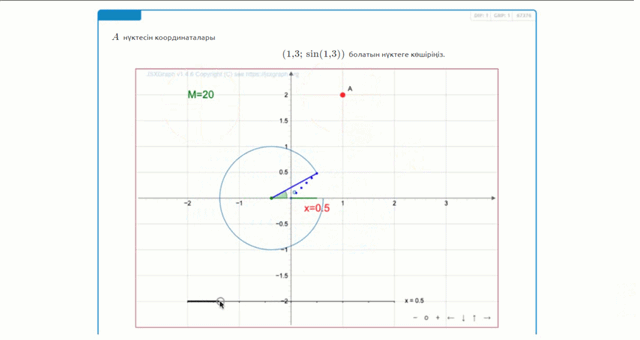
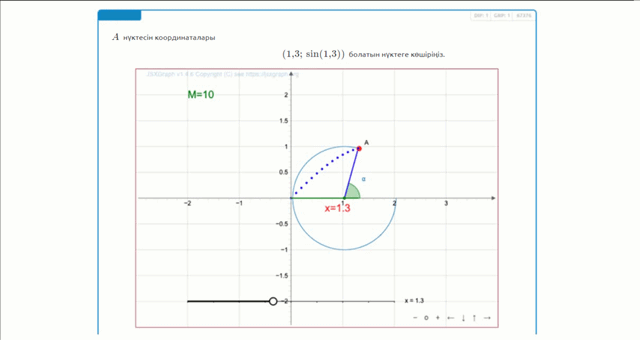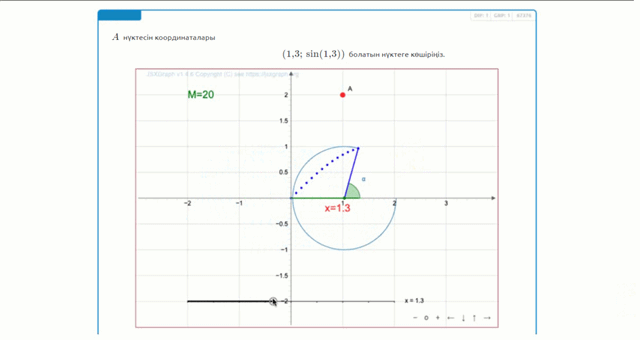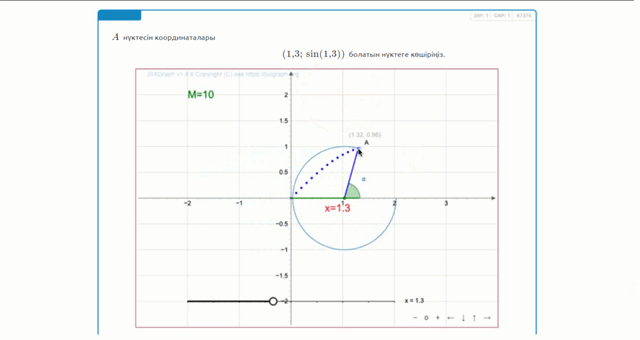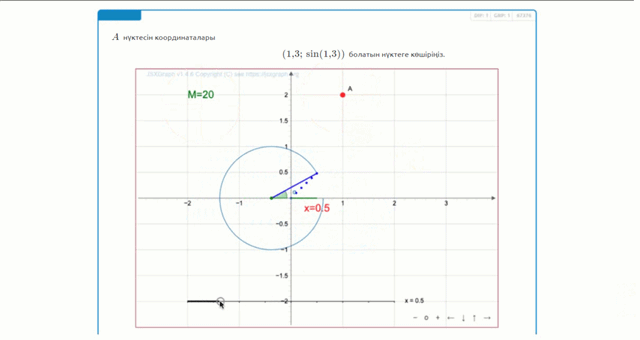
Координасы \(\displaystyle x=1{,}3\) бірлікке тең нүкте алу үшін, \(\displaystyle x\)-ті \(\displaystyle 1{,}3{\small}\)-ке орналастыру керек.
Құрылымы бойынша бірлік шеңберде жоғалған доғаның ұзындығы \(\displaystyle 1{,}3\) радианға тең.
Яғни, біз \(\displaystyle 1{,}3\) радианға тең бұрыш алдық.
Осылайша, нүкте шеңбер бойымен қозғалғанда \(\displaystyle 1{,}3\) радианға тең бұрыш пайда болады.
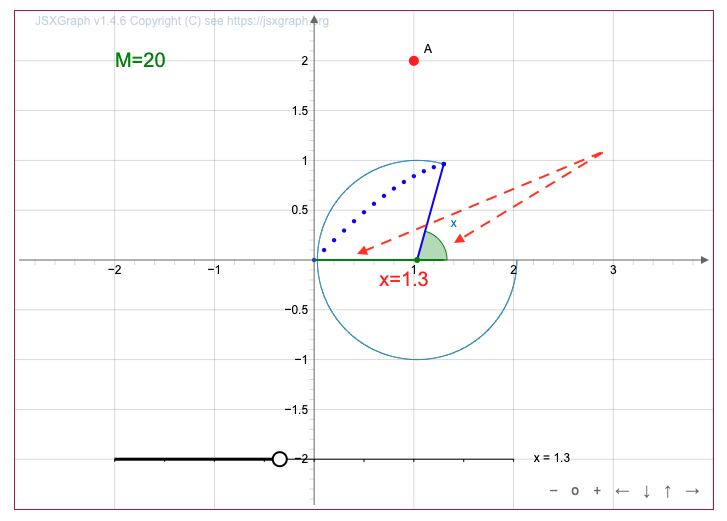
Нүкте бірлік шеңберде жатқандықтан, \(\displaystyle y\) координатасы \(\displaystyle \sin(1{,}3){\small}\)-ға тең.

Демек, координаталары төмендегідей болатын нүктені аламыз
\(\displaystyle (1{,}3;\,\sin(1{,}3) ){\small .}\)
Тексеру мәні \(\displaystyle M=10{\small .}\)