Теріс дискриминанты бар квадраттық функцияны таңдаңыз.
\(\displaystyle y=ax^2+bx+c\) параболада \(\displaystyle ax^2+bx+c=0 {\small } \) квадрат теңдеудің түбірі болатын нүктелерді анықтаңыз
\(\displaystyle ax^2+bx+c=0{ \small ,} \) болғандықтан, бұлар параболадағы нүктелер, олар үшін \(\displaystyle y=0{ \small } \) \(\displaystyle y=0{ \small ,} \) нүктелері де осьте \(\displaystyle \rm OX{\small } \) жатады
Яғни, бір жағынан, нүктелер параболада, ал екінші жағынан, \(\displaystyle \rm OX{\small } \) осьте жатады Демек, бұл параболаның \(\displaystyle \rm OX {\small }\) осімен қиылысу нүктелері
Біз ықтимал жағдайларды тізімдейміз:
Параболаның \(\displaystyle \rm OX \) осімен қиылысу нүктелерінің саны | Квадрат теңдеудің түбірлерінің саны |
Екі қиылысу нүктесі | Екі шешім |
Бір қиылысу нүктесі (осьтің жанасуы) | Бір шешім |
Қиылысу нүктелері жоқ | Шешімдер жоқ |
Немесе дискриминант тұрғысынан:
Параболаның қиылысу нүктелерінің саны \(\displaystyle \rm OX \) осімен | Дискриминант белгісі \(\displaystyle \rm D \) |
Екі қиылысу нүктесі | \(\displaystyle {\rm D}>0 \) |
Бір қиылысу нүктесі (осьтің жанасуы) | \(\displaystyle {\rm D}=0 \) |
Қиылысу нүктелері жоқ | \(\displaystyle {\rm D}<0 \) |
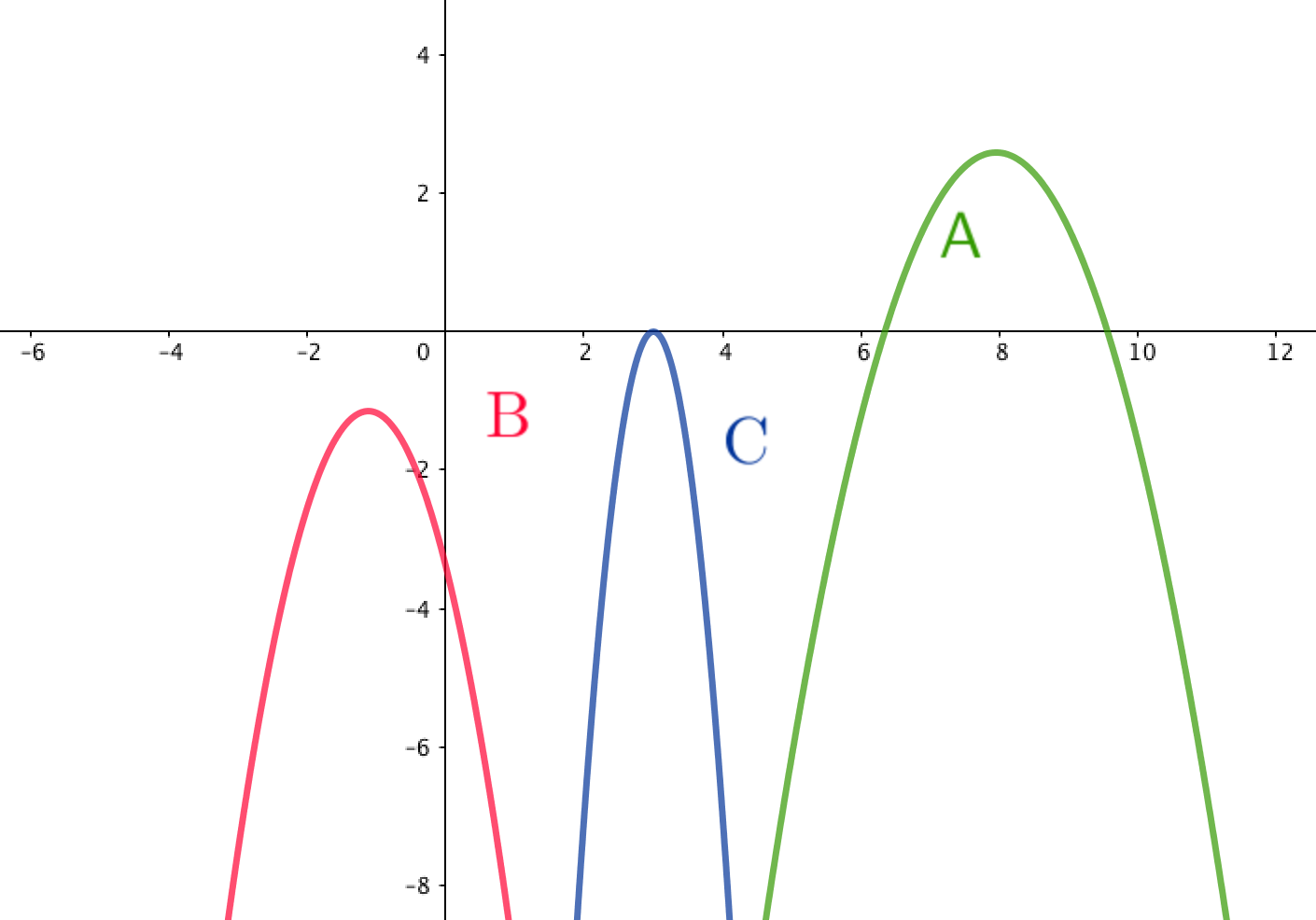
Есептің шартынан суреттегі теріс дискриминанты бар квадраттық функцияларды табайық.
Бұл \(\displaystyle \rm OX{\small } \) осьпен қиылысу нүктелері жоқ параболалар

Тек параболаның \(\displaystyle \rm OX \) осімен қиылысу нүктелері \(\displaystyle \rm \color{red}{ B}{\small } \) жоқ.
Жауабы: \(\displaystyle \rm \color{red}{ B}{\small .} \)