Представьте угол \(\displaystyle -780^{\circ}\) в виде \(\displaystyle a+360^{\circ}\cdot n{\small,}\) где число \(\displaystyle n\) целое и \(\displaystyle a\) от \(\displaystyle \color{red}{0}^{\circ}\) до \(\displaystyle \color{red}{360}^{\circ}\)\(\displaystyle (0^{\circ}\le a<360^{\circ}){\small.}\) Выберите числа \(\displaystyle a\) и \(\displaystyle n\) из списка.
\(\displaystyle -780^{\circ}=\)\(\displaystyle {}^\circ+\)\(\displaystyle 360^{\circ}\cdot(\)\(\displaystyle )\)
Поворот на \(\displaystyle -780^{\circ}\) – это поворот на \(\displaystyle 780^{\circ}{ \small ,}\) только в другом направлении.
Поэтому сначала можно найти число полных оборотов и угол поворота после них для \(\displaystyle 780^{\circ}{\small.}\)
Для этого поделим \(\displaystyle 780\) на \(\displaystyle \color{red}{360}\) с остатком:
\(\displaystyle 780=2\cdot \color{red}{360}+60{\small.}\)
Значит,
\(\displaystyle 780^{\circ}=60^{\circ}+\color{red}{360}^{\circ}\cdot 2{\small.}\)
Поскольку изначально поворот был в отрицательном направлении, то ставим знак "минус" перед обеими частями равенства и получаем:
\(\displaystyle -(780^{\circ})=-(60^{\circ}+360^{\circ}\cdot 2){\small.}\)
Раскрывая скобки, получаем:
\(\displaystyle -780^{\circ}=\color{blue}{-60^{\circ}}+{360^{\circ}\cdot (-2)}{\small.}\)
Число \(\displaystyle \color{blue}{-60^{\circ}}\) не попало в интервал от \(\displaystyle 0^{\circ}\) до \(\displaystyle 360^{\circ}{\small:}\)
Чтобы это исправить, прибавим и вычтем \(\displaystyle 360^{\circ}{\small:}\)
\(\displaystyle -780^{\circ}=\color{blue}{-60^{\circ}}+\color{red}{360^{\circ}}-\color{red}{360^{\circ}}+{360^{\circ}\cdot(-2)}=\color{blue}{300}^{\circ}+360^{\circ}\cdot(\color{green}{-3}){\small.}\)
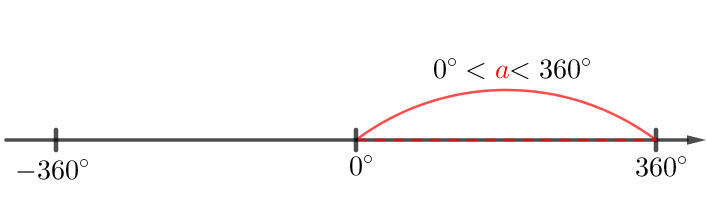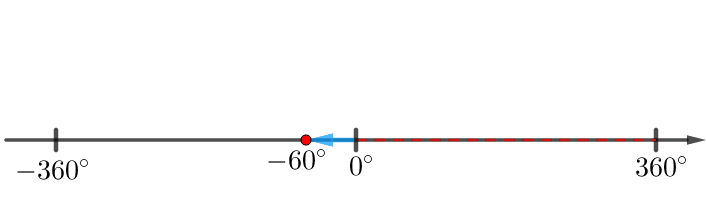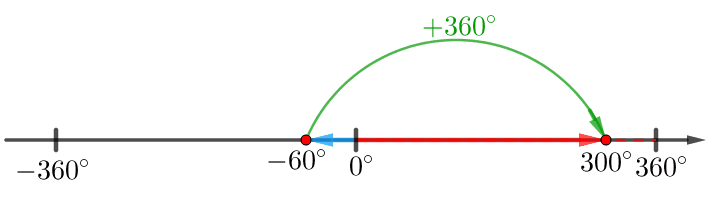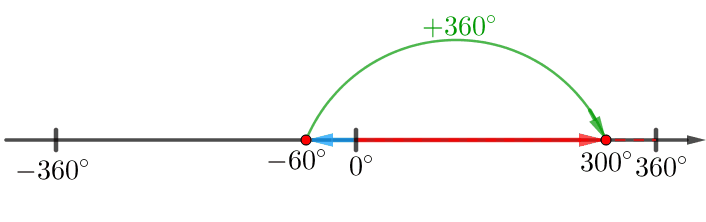
То есть \(\displaystyle \color{blue}{a}=\color{blue}{300}^\circ\) и \(\displaystyle \color{green}{n}=\color{green}{-3}{\small.}\)