\(\displaystyle -780^{\circ}\) бұрышын \(\displaystyle a+360^{\circ}\cdot n{\small}\) түрінде көрсетіңіз, мұндағы \(\displaystyle n\) бүтін сан және \(\displaystyle a\) \(\displaystyle \color{red}{0}^{\circ}\) бастап \(\displaystyle \color{red}{360}^{\circ}\) дейін \(\displaystyle (0^{\circ}\le a<360^{\circ}){\small.}\) Тізімнен \(\displaystyle a\) және \(\displaystyle n\) сандарын таңдаңыз.
\(\displaystyle -780^{\circ}=\)\(\displaystyle {}^\circ+\)\(\displaystyle 360^{\circ}\cdot(\)\(\displaystyle )\)
\(\displaystyle -780^{\circ}\) айналу – бұл \(\displaystyle 780^{\circ}{ \small }\) тек басқа бағытта айналу.
Сондықтан алдымен толық айналымдар санын және олардан кейінгі \(\displaystyle 780^{\circ}{\small}\) айналу бұрышын табуға болады.
Ол үшін \(\displaystyle 780\) қалдығымен \(\displaystyle \color{red}{360}\) бөлеміз:
\(\displaystyle 780=2\cdot \color{red}{360}+60{\small.}\)
Демек,
\(\displaystyle 780^{\circ}=60^{\circ}+\color{red}{360}^{\circ}\cdot 2{\small.}\)
Айналу бастапқыда теріс бағытта болғандықтан, теңдіктің екі бөлігінің алдына "минус" белгісін қойып, мынаны аламыз:
\(\displaystyle -(780^{\circ})=-(60^{\circ}+360^{\circ}\cdot 2){\small.}\)
Жақшаларды ашып, біз мынаны аламыз:
\(\displaystyle -780^{\circ}=\color{blue}{-60^{\circ}}+{360^{\circ}\cdot (-2)}{\small.}\)
\(\displaystyle \color{blue}{-60^{\circ}}\) саны \(\displaystyle 0^{\circ}\) бастап \(\displaystyle 360^{\circ}{\small}\) дейінгі интервалына кірмеді:
Мұны түзету үшін \(\displaystyle 360^{\circ}{\small}\) қосамыз және азайтамыз:
\(\displaystyle -780^{\circ}=\color{blue}{-60^{\circ}}+\color{red}{360^{\circ}}-\color{red}{360^{\circ}}+{360^{\circ}\cdot(-2)}=\color{blue}{300}^{\circ}+360^{\circ}\cdot(\color{green}{-3}){\small.}\)
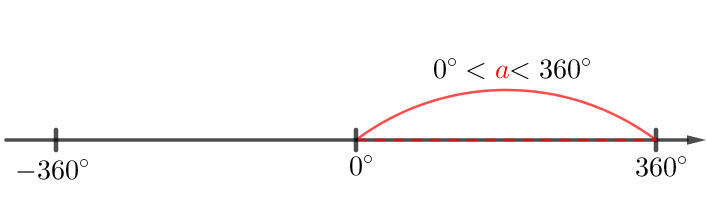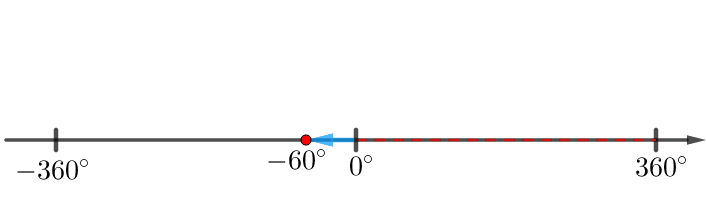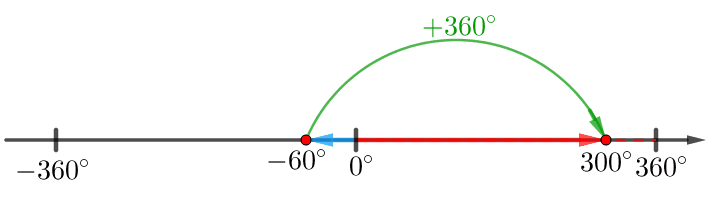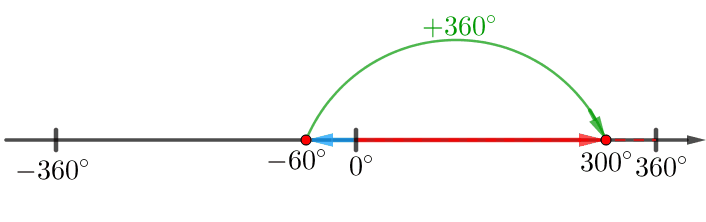
Яғни \(\displaystyle \color{blue}{a}=\color{blue}{300}^\circ\) және \(\displaystyle \color{green}{n}=\color{green}{-3}{\small.}\)