На рисунке изображён график функции \(\displaystyle f\left(x\right)=k\sqrt{x}.\) Найдите значение \(\displaystyle x,\) при котором \(\displaystyle f\left(x\right)=3{,}5.\)

\(\displaystyle x=\)
Чтобы найти значения \(\displaystyle x{\small ,}\) при которых \(\displaystyle f(x)=3{,}5{ \small ,}\)
- найдём неизвестный коэффициент \(\displaystyle k{ \small ,}\)
- решим уравнение \(\displaystyle k\sqrt{x}=3{,}5{ \small .}\)
Заметим, что на графике функции \(\displaystyle f\left(x\right)=k\sqrt{x}\) отмечена точка с координатами \(\displaystyle (\color{blue}{4};\color{blue}{5}){ \small .}\)
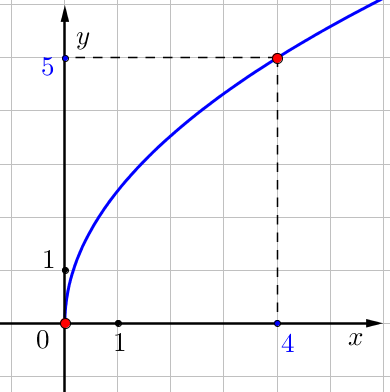
Значит, при подстановке её координат \(\displaystyle x=\color{blue}4\) и \(\displaystyle y=\color{blue}5\) в уравнение \(\displaystyle y=k\cdot \sqrt{x}\)
получим верное равенство.
Подставляя, получаем уравнение:
\(\displaystyle \color{blue}5=k\cdot \sqrt{\color{blue}4}{ \small ,} \)
\(\displaystyle 5=k \cdot 2{ \small ,} \)
откуда
\(\displaystyle {k}=2{,}5{ \small .}\)
Таким образом, исходная функция имеет вид:
\(\displaystyle f\left(x\right)=2{,}5\sqrt{x} \small.\)
Найдём те значения \(\displaystyle x{ \small ,}\) при которых значения функции \(\displaystyle f(x)\) равны \(\displaystyle 3{,}5{ \small .}\)
Все такие \(\displaystyle x\) удовлетворяют уравнению
\(\displaystyle 2{,}5\cdot \sqrt{x}=3{,}5{\small .}\)
Приведем данное уравнение к элементарному виду:
\(\displaystyle 2{,}5 \cdot \sqrt{x}=3{,}5\ \ \ \color{red}{\bigg | : 2{,}5}{\small ,}\)
\(\displaystyle \sqrt{x}=1{,}4{\small .}\)
Для того чтобы решить иррациональное уравнение, воспользуемся правилом:
Уравнение вида \(\displaystyle \sqrt{f(x)}=a\)
- Если \(\displaystyle a \geq 0\small,\) то уравнение \(\displaystyle \sqrt{f(x)}=a \) равносильно уравнению \(\displaystyle f(x)=a^2 \small;\ \\ \)
- если \(\displaystyle a < 0\small,\) то уравнение \(\displaystyle \sqrt{f(x)}=a \) не имеет действительных решений.
Тогда
\(\displaystyle x=(1{,}4)^2\small,\)
\(\displaystyle x=1{,}96\small.\)
Ответ: \(\displaystyle 1{,}96{\small .}\)