Суретте \(\displaystyle f\left(x\right)=k\sqrt{x}\) функциясының графигі көрсетілген \(\displaystyle x\) болатын\(\displaystyle f\left(x\right)=3{,}5\) мәнін табыңыз.

\(\displaystyle x=\)
\(\displaystyle x{\small}\) болатын \(\displaystyle f(x)=3{,}5{ \small }\) мәндерін табу үшін
- белгісіз \(\displaystyle k{ \small}\) коэффициентті табыңыз
- \(\displaystyle k\sqrt{x}=3{,}5{ \small }\) теңдеуді шешеміз
\(\displaystyle f\left(x\right)=k\sqrt{x}\) функциясының графигінде \(\displaystyle (\color{blue}{4};\color{blue}{5}){ \small}\) координаттары бар нүкте белгіленгенін ескеріңіз.
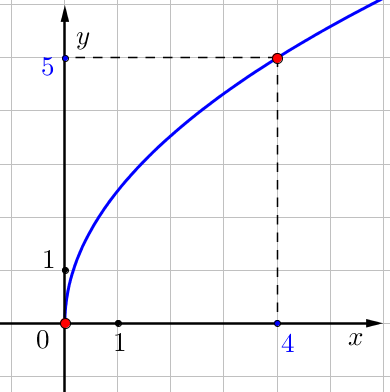
Сонымен, оның \(\displaystyle x=\color{blue}4\) және \(\displaystyle y=\color{blue}5\) координаттарын \(\displaystyle y=k\cdot \sqrt{x}\)
теңдеуіне ауыстырған кезде дұрыс теңдік аламыз.
Қоя отырып, теңдеу аламыз:
\(\displaystyle \color{blue}5=k\cdot \sqrt{\color{blue}4}{ \small ,} \)
\(\displaystyle 5=k \cdot 2{ \small ,} \)
қайдан
\(\displaystyle {k}=2{,}5{ \small .}\)
Осылайша, бастапқы функция келесідей болады:
\(\displaystyle f\left(x\right)=2{,}5\sqrt{x} \small.\)
\(\displaystyle x{ \small }\) функциясының мәндері \(\displaystyle f(x)\) \(\displaystyle 3{,}5{ \small }\) болатын мәндерді табайық
Барлық осындай \(\displaystyle x\) теңдеуді қанағаттандырады
\(\displaystyle 2{,}5\cdot \sqrt{x}=3{,}5{\small .}\)
Бұл теңдеуді қарапайым түрге келтірейік:
\(\displaystyle 2{,}5 \cdot \sqrt{x}=3{,}5\ \ \ \color{red}{\bigg | : 2{,}5}{\small ,}\)
\(\displaystyle \sqrt{x}=1{,}4{\small .}\)
Иррационал теңдеуді шешу үшін біз ережені қолданамыз:
түрінде теңдеу \(\displaystyle \sqrt{f(x)}=a\)
- Егер \(\displaystyle a \geq 0\small,\) онда \(\displaystyle \sqrt{f(x)}=a \) теңдеуі \(\displaystyle f(x)=a^2 \small\ \\ \) теңдеуіне тең;
- Егер \(\displaystyle a < 0\small,\) онда \(\displaystyle \sqrt{f(x)}=a \) теңдеуінің жарамды шешімдері жоқ.
Онда
\(\displaystyle x=(1{,}4)^2\small,\)
\(\displaystyle x=1{,}96\small.\)
Жауабы: \(\displaystyle 1{,}96{\small .}\)