Суретте \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+b}+c\small\) функцияның графигі көрсетілген \(\displaystyle x\small,\) \(\displaystyle f\left(x\right)=8\small\) мәнін табыңыз.
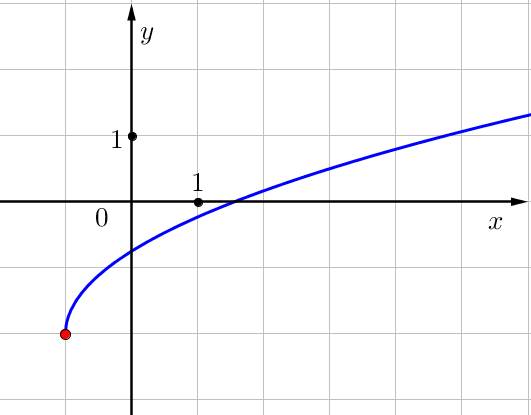
\(\displaystyle x=\)
\(\displaystyle x\small\) болатын \(\displaystyle f\left(x\right)=8\small\) мәнін табу үшін
- Белгісіз \(\displaystyle \color{blue}b\) және \(\displaystyle \color{green}c\small\) коэффициентін табамыз
- \(\displaystyle \frac{5}{4} \cdot \sqrt{x+\color{blue}b}+\color{green}c=8\small\) теңдеуді шешеміз
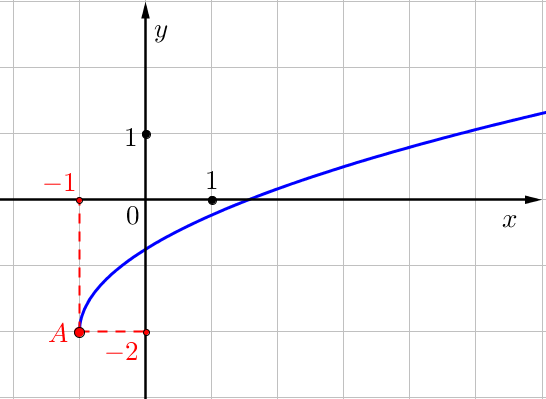
\(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{b}}+\color{green}c\) функция графигінде белгіленген нүктені\(\displaystyle \color{red}A\small\) әріппен белгілеңіз.
Оның координаталарын анықтаймыз:
\(\displaystyle x_0=\color{red}{-1}\) – абсцисса, \(\displaystyle y_0=\color{red}{-2}\) – нүкте ординатасы \(\displaystyle \color{red}A\small.\)
\(\displaystyle \color{blue}{b}\small\) мәнін табамыз.
График бойынша \(\displaystyle x_0=\color{red}{-1}\) нүктенің \(\displaystyle \color{red}{A} \) абсциссасы \(\displaystyle x\) функцияны анықтау аймағындағы айнымалының \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{b}}+\color{green}c \small\) ең кіші мәніне тең.
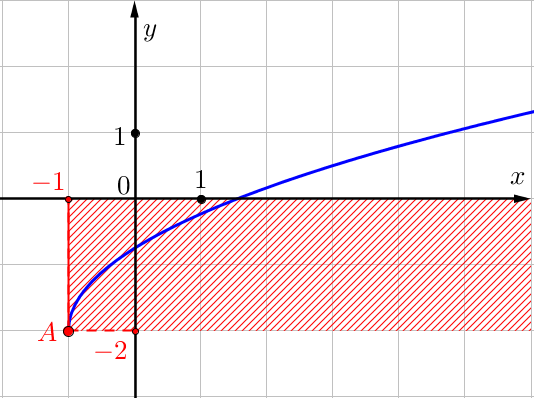
Осы функцияның анықталу аймағын табыңыз.
Ережені қолданамыз:
Егер \(\displaystyle a\) теріс емес болса, \(\displaystyle a\) санының түбірі (нақты сандарда) бар.
Яғни \(\displaystyle \sqrt{a}\) бар, егер \(\displaystyle a \geq 0 \small.\)
Біздің жағдайда
\(\displaystyle x+\color{blue}{b} \geq 0\small.\)
Қайдан
\(\displaystyle x \geq -\color{blue}b\small.\)
Демек, \(\displaystyle x=-\color{blue}b \) – функцияны анықтау аймағындағы айнымалының ең кіші мәні.
Демек,
\(\displaystyle -\color{blue}b=\color{red}{-1} \small, \)
\(\displaystyle \color{blue}b=\color{blue}1 \small. \)
табылған \(\displaystyle \color{blue}b\) мәнін тауып, аламыз:
\(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\small.\)
\(\displaystyle \color{green}c\small\) мәнін табамыз.
\(\displaystyle \color{red}{A(-1;-2)} \) нүктесі \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\small\) функция графигінде жатыр
Демек, \(\displaystyle x=\color{red}{-1}\) және \(\displaystyle y=\color{red}{-2}\) координаттарын \(\displaystyle y=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\) теңдеуге қойған кезде, дұрыс теңдік аламыз.
Осылайша теңдеу аламыз:
\(\displaystyle \color{red}{-2}=\frac{5}{4}\sqrt{\color{red}{-1}+\color{blue}1}+\color{green}c\small,\)
қайдан
\(\displaystyle \color{green}c=\color{green}{-2} \small.\)
\(\displaystyle \color{green}c=\color{green}{-2}{} \) қоямыз:
\(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{1}}\color{green}{-2}\small.\)
\(\displaystyle x\small\) болғанда, \(\displaystyle f\left(x\right)=8\small\) мәнін табамыз.
Ол үшін теңдеуді шешу керек
\(\displaystyle \frac{5}{4}\cdot \sqrt{x+1}-2=8\small.\)
Жауабы: \(\displaystyle 63{\small.}\)