Digital Matematika - 8 сынып - Квадрат түбір функциясының коэффициенттерін анықтау

Тапсырма

Суретте \(\displaystyle f\left(x\right)=k\sqrt{x+b}-\frac{5}{4} \small\) функциясының графигі көрсетілген \(\displaystyle x \small\) болатын \(\displaystyle f\left(x\right)=\frac{5}{4} \small\) мәнін табыңыз.

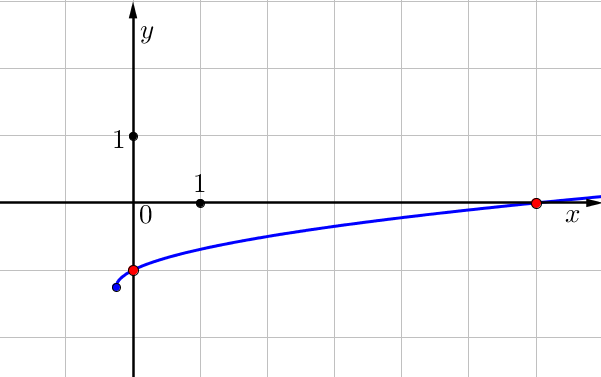
\(\displaystyle x=\)

Шешім

\(\displaystyle x\small\) болатын\(\displaystyle f\left(x\right)=\frac{5}{4} \small\) мәнін табу үшін

\(\displaystyle \color{blue}b\) және \(\displaystyle \color{orange}k\small\) белгісіз коэффициенттерді табыңыз
теңдеуді шешеміз \(\displaystyle \color{orange}k \cdot \sqrt{x+\color{blue}b}-\frac{5}{4}=\frac{5}{4}\small.\)

\(\displaystyle f\left(x\right)=\color{orange}{k}\sqrt{x+\color{blue}b}-\frac{5}{4}\) функциясының графигіндегі белгіленген нүктелерді\(\displaystyle \color{red}A\) және \(\displaystyle \color{Magenta}B \small\) әріптерімен белгілейік

Осы нүктелердің координаттарын анықтайық:

\(\displaystyle x_1=\color{red}{0}\) – абсцисса, \(\displaystyle y_1=\color{red}{-1}\) – нүкте ординатасы \(\displaystyle \color{red}A\small,\)
\(\displaystyle x_2=\color{Magenta}{6}\) – абсцисса, \(\displaystyle y_2=\color{Magenta}{0}\) – нүкте ординатасы \(\displaystyle \color{Magenta}B\small.\)

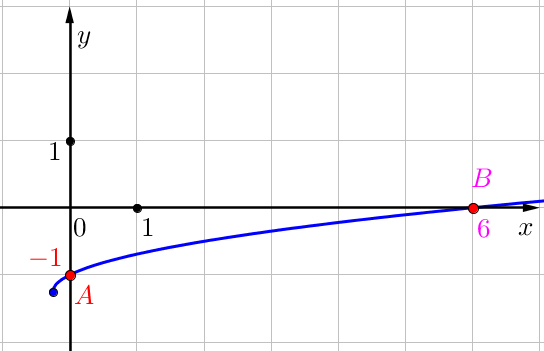
\(\displaystyle \color{red}{A(0;-1)}\) және \(\displaystyle \color{Magenta}{B(6;0)}\) нүктелері \(\displaystyle f\left(x\right)=\color{orange}{k}\sqrt{x+\color{blue}b}-\frac{5}{4}\small\) функция графиктерінде жатыр.

Демек,

\(\displaystyle x=\color{red}{0}\) және \(\displaystyle y=\color{red}{-1}\) \(\displaystyle y=\color{orange}{k}\sqrt{x+\color{blue}{b}}-\frac{5}{4}\) теңдеуіне ауыстырған кезде біз бірінші дұрыс теңдікті аламыз,
\ \(\displaystyle x=\color{Magenta}{6}\) және \(\displaystyle y=\color{Magenta}{0}\) \(\displaystyle y=\color{orange}{k}\sqrt{x+\color{blue}{b}}-\frac{5}{4}\) теңдеуіне ауыстырған кезде біз екінші дұрыс теңдікті аламыз.

Нәтижесінде теңдеулер жүйесін аламыз:

\(\displaystyle\left\{\begin{aligned}\color{red}{-1}&=\color{orange}{k} \cdot \sqrt{\color{red}{0}+\color{blue}{b}}-\frac{5}{4}{\small,} \\[10px]\color{Magenta}{0}&=\color{orange}{k} \cdot \sqrt{\color{Magenta}{6}+\color{blue}{b}}-\frac{5}{4}{\small.}\end{aligned}\right.\)

Алынған жүйені шешеміз. \(\displaystyle b=\frac{1}{4}\small,\ \ k=\frac{1}{2} \small.\)

Біз бұл жүйені келесі түрде жазамыз:

\(\displaystyle\left\{\begin{aligned}&k \cdot \sqrt{b}=\frac{5}{4}-1{\small,} \\[10px]&k \cdot \sqrt{b+6}=\frac{5}{4}{\small;}\end{aligned}\right.\)

\(\displaystyle\left\{\begin{aligned}&k \cdot \sqrt{b}=\frac{1}{4}{\small,} \\[10px]&k \cdot \sqrt{b+6}=\frac{5}{4}{\small.}\end{aligned}\right.\)

Жүйенің бірінші теңдеуінен \(\displaystyle k\) арқылы\(\displaystyle b\) \(\displaystyle \big( \)көрсетеміз \(\displaystyle b \ \cancel= \ 0\)\(\displaystyle \big) \small\) байқаймыз

\(\displaystyle k \cdot \sqrt{b}=\frac{1}{4} \ \ \color{red}{\bigg|: \sqrt{b}}{\small,}\)

\(\displaystyle k=\frac{1}{4 \cdot \sqrt{b}}\small.\)

Жүйенің екінші теңдеуінде \(\displaystyle k\) орнына \(\displaystyle \frac{1}{4 \cdot \sqrt{b}}\small\) өрнегін қоямыз

\(\displaystyle \frac{1}{4 \cdot \sqrt{b}} \cdot \sqrt{b+6}=\frac{5}{4}\small, \)

\(\displaystyle \frac{\sqrt{b+6}}{4 \cdot \sqrt{b}}=\frac{5}{4} \ \ \ \color{red}{\bigg| \cdot 4\sqrt{b} } \small, \)

\(\displaystyle \sqrt{b+6}=\frac{5 \cdot 4 \cdot \sqrt{b}}{4}\small, \)

\(\displaystyle \sqrt{b+6}=5 \cdot \sqrt{b}\small. \)

Бұл \(\displaystyle b+6\geqslant 0\) және \(\displaystyle b\geqslant 0{ \small ,} \) теңдеу үшін кайтадан \(\displaystyle b\geqslant 0{\small .} \)

Теңдеудің екі бөлігін де квадраттайық:

\(\displaystyle \bigg( \sqrt{b+6}\bigg)^2=\bigg(5 \cdot \sqrt{b}\bigg)^2\small, \)

\(\displaystyle b+6=25 \cdot b\small, \)

\(\displaystyle 6=25 \cdot b-b\small, \)

\(\displaystyle 24 \cdot b=6\small, \)

\(\displaystyle b=\frac{6}{24} \small,\)

\(\displaystyle b=\frac{1}{4} \small.\)

\(\displaystyle b\geqslant 0 \) және \(\displaystyle b=\frac{1}{4}\geqslant 0 \small,\) болғандықтан \(\displaystyle b=\frac{1}{4} \) – теңдеу түбірі.

\(\displaystyle k\small\) мәнін табамыз.

Ол үшін \(\displaystyle k=\frac{1}{4 \cdot \sqrt{b}}\) теңдеуінде\(\displaystyle b\) орнына \(\displaystyle \frac{1}{4} \small\) қоямыз

\(\displaystyle k=\frac{1}{4 \cdot \sqrt{ \frac{1}{4}}} \small,\)

\(\displaystyle k=\frac{1}{4 \cdot \frac{1}{2}} \small,\)

\(\displaystyle k=\frac{1}{2} \small.\)

Осылайша, бастапқы функция келесідей болады:

\(\displaystyle f\left(x\right)=\color{orange}{\frac{1}{2}}\sqrt{x+\color{blue}{\frac{1}{4}}}-\frac{5}{4} \small.\)

\(\displaystyle x\small \) болғанда \(\displaystyle f\left(x\right)=\frac{5}{4} \small.\)

\(\displaystyle x=24{,}75 \small.\)

Жауабы:\(\displaystyle 24{,}75 \small.\)

Теориясы: 04 Квадрат түбір функциясының коэффициенттерін анықтау

Уравнение вида \(\displaystyle \sqrt{f(x)}=a\)