Задание
Определите число отрезков на рисунке с концами в обозначенных точках.
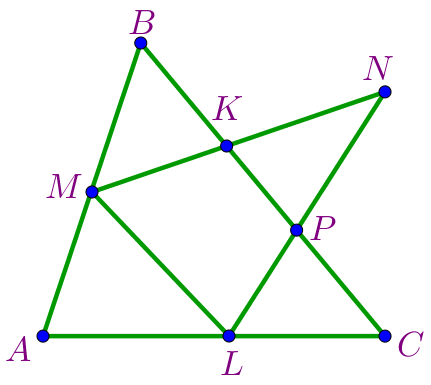
Количество отрезков равно
Решение
Определим количество отрезков на каждой прямой, проходящей через обозначенные точки.
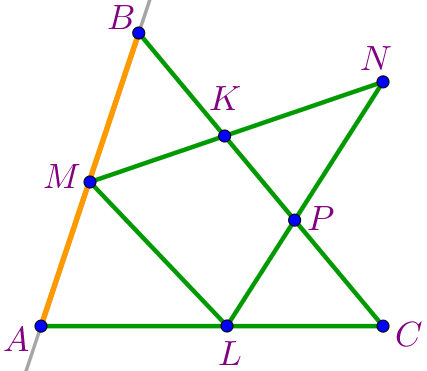 | На прямой \(\displaystyle AB\) три точки \(\displaystyle A{\small,}\) \(\displaystyle M\) и \(\displaystyle B\) образуют три отрезка \(\displaystyle AM{\small,}\) \(\displaystyle AB\) и \(\displaystyle MB{\small.}\) |
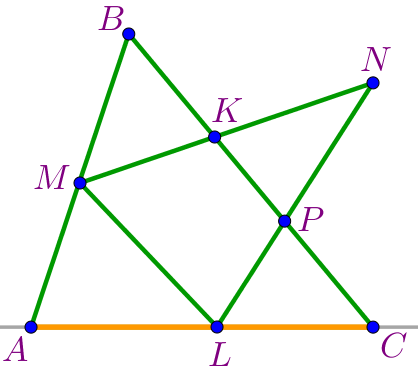 | На прямой \(\displaystyle AC\) три точки \(\displaystyle A{\small,}\) \(\displaystyle L\) и \(\displaystyle C\) образуют три отрезка \(\displaystyle AL{\small,}\) \(\displaystyle AC\) и \(\displaystyle LC{\small.}\) |
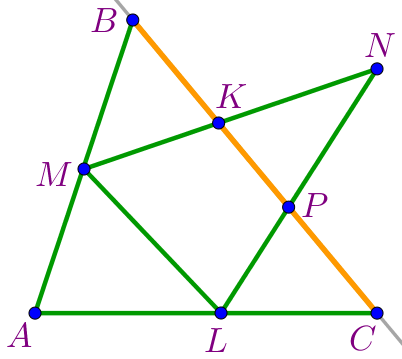 | На прямой \(\displaystyle BC\) четыре точки \(\displaystyle B{\small,}\) \(\displaystyle K{\small,}\) \(\displaystyle P\) и \(\displaystyle C\) образуют шесть отрезков \(\displaystyle BK{\small,}\) \(\displaystyle BP{\small,}\) \(\displaystyle BC{\small,}\) \(\displaystyle KP{\small,}\) \(\displaystyle KC\) и \(\displaystyle PC{\small.}\) |
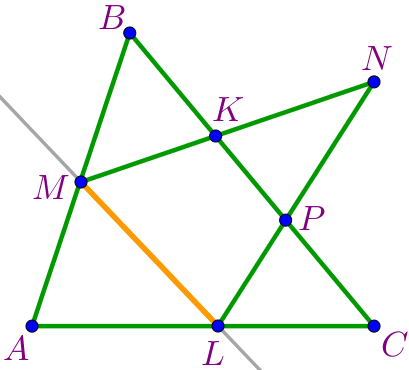 | На прямой \(\displaystyle ML\) две точки \(\displaystyle M\) и \(\displaystyle L\) образуют один отрезок \(\displaystyle ML{\small.}\) |
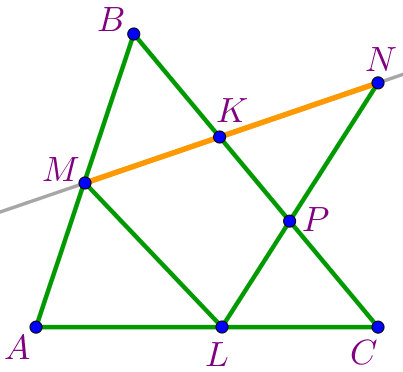 | На прямой \(\displaystyle MN\) три точки \(\displaystyle M{\small,}\) \(\displaystyle K\) и \(\displaystyle N\) образуют три отрезка \(\displaystyle MK{\small,}\) \(\displaystyle MN\) и \(\displaystyle KN{\small.}\) |
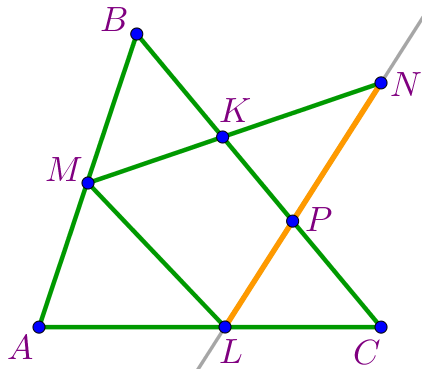 | На прямой \(\displaystyle LN\) три точки \(\displaystyle L{\small,}\) \(\displaystyle P\) и \(\displaystyle N\) образуют три отрезка \(\displaystyle LP{\small,}\) \(\displaystyle LN\) и \(\displaystyle PN{\small.}\) |
Посчитаем общее количество отрезков с концами в обозначенных точках:
\(\displaystyle 3+3+6+1+3+3=19 {\small.}\)
Ответ: \(\displaystyle 19\)