На прямой отметили \(\displaystyle n\) точек. Сколько всего получилось отрезков с концами в отмеченных точках?
Обозначим точки на прямой \(\displaystyle A_1{\small,}\) \(\displaystyle A_2{\small,}\) \(\displaystyle \ldots {\small,}\) \(\displaystyle A_n{\small.}\)
Точка \(\displaystyle A_1\) образует \(\displaystyle (n-1)\) различных отрезков с остальными точками: \(\displaystyle A_1A_2{\small,}\) \(\displaystyle A_1A_3{\small,}\) \(\displaystyle A_1A_4{\small,}\) \(\displaystyle \ldots {\small,}\) \(\displaystyle A_1A_n{\small.}\)
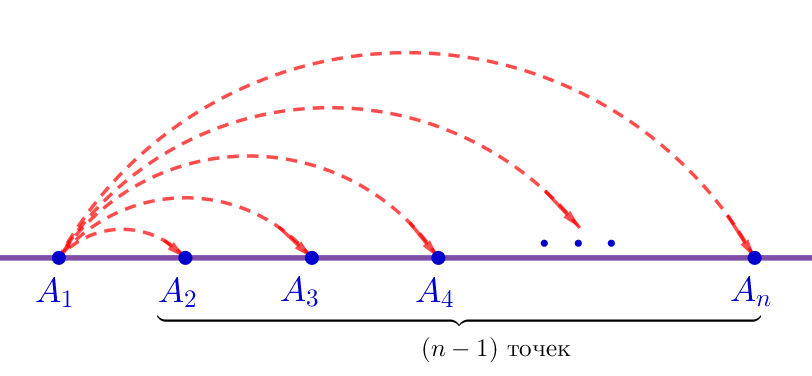
То есть количество отрезков с концом в точке \(\displaystyle A_1\) равно \(\displaystyle n-1 {\small.}\)
Аналогично, для каждой точки \(\displaystyle A_i\) получаем: количество отрезков с концом в данной точке равно \(\displaystyle n-1 {\small.}\)
Всего точек \(\displaystyle n{\small.}\) Тогда можно предположить, что \(\displaystyle n\cdot(n-1)\) – это количество отрезков, которые образуют \(\displaystyle n\) точек. Но при таком подсчёте получается, что каждый отрезок учитывается дважды: сначала его посчитали для одного конца, а потом ещё раз посчитали для другого конца. Для верного вычисления количества отрезков нужно произведение \(\displaystyle n\cdot(n-1)\) поделить на \(\displaystyle 2{\small.}\)
Получили формулу для вычисления количества различных отрезков с концами в заданных точках.
Если на прямой отметить \(\displaystyle n\) точек, то образуется \(\displaystyle k=\frac{n \cdot (n-1)}{2}\) отрезков с концами в отмеченных точках.
Ответ: \(\displaystyle \frac{n \cdot (n-1)}{2}\)