\(\displaystyle n\) нүктелер түзу сызықта белгіленді. Белгіленген нүктелерде неше кесіндіні болды?
\(\displaystyle A_1{\small,}\) \(\displaystyle A_2{\small,}\) \(\displaystyle \ldots {\small,}\) \(\displaystyle A_n{\small}\) түзудегі нүктелерді белгілеңіз.
\(\displaystyle A_1\) нүктесі \(\displaystyle (n-1)\) басқа нүктелерімен әртүрлі кесінділерді құрайды: \(\displaystyle A_1A_2{\small,}\) \(\displaystyle A_1A_3{\small,}\) \(\displaystyle A_1A_4{\small,}\) \(\displaystyle \ldots {\small,}\) \(\displaystyle A_1A_n{\small.}\)
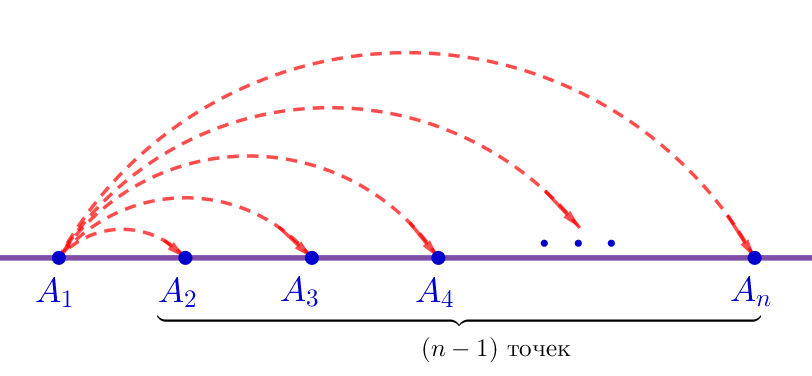
Яғни \(\displaystyle A_1\) нүктесінде аяқталатын кесінділер саны \(\displaystyle n-1 {\small}\) тең.
Сол сияқты, әрбір нүкте үшін \(\displaystyle A_i\) аламыз: осы нүктеде аяқталатын кесінділер саны\(\displaystyle n-1 {\small}\) тең.
Жалпы\(\displaystyle n{\small}\) нүкте. Сонда \(\displaystyle n\cdot(n-1)\) \\(\displaystyle n\) нүктені құрайтын кесінділер саны деп есептей аламыз. Бірақ мұндай есептеу арқылы әрбір кесінді екі рет есептелетіні белгілі болды: алдымен ол бір ұшы үшін саналды, содан кейін ол екінші ұшы үшін қайта есептелді. Кесінділердің санын дұрыс есептеу үшін \(\displaystyle n\cdot(n-1)\) көбейтіндіні \(\displaystyle 2{\small}\) бөлу керек.
Біз берілген нүктелерде ұштары бар әртүрлі кесінділердің санын есептеу формуласын алдық.
Егер \(\displaystyle n\) нүктелер түзуде белгіленсе, онда \(\displaystyle k=\frac{n \cdot (n-1)}{2}\) белгіленген нүктелерде ұштары бар кесінділер түзіледі.
Жауабы: \(\displaystyle \frac{n \cdot (n-1)}{2}\)