Төмендегі тұжырымдардың қайсысы дұрыс?
\(\displaystyle 1)\) Трапецияның диагональдары қиылысады және қиылысу нүктесімен екіге бөлінеді.
\(\displaystyle 2)\) Шеңбердің барлық диаметрлері тең.
\(\displaystyle 3)\) Үшбұрыштың бір бұрышы әрқашан \(\displaystyle 60\) градустан кіші.
Жауап ретінде таңдалған тұжырымдардың сандарын бос орынсыз, үтір немесе басқа қосымша таңбаларсыз жазыңыз.
Әрбір тұжырымды қарастырайық:
\(\displaystyle 1)\) Трапецияның диагональдары қиылысады және қиылысу нүктесімен екіге бөлінеді.
Трапеция үшін келесі тұжырым дұрыс:
Трапецияның диагональдары қиылысады және қиылысу нүктесі арқылы трапеция табандарына пропорционал кесінділерге бөлінеді. \(\displaystyle \frac{AO}{OC}= \frac{DO}{OB}= \frac{AD}{BC}\) | 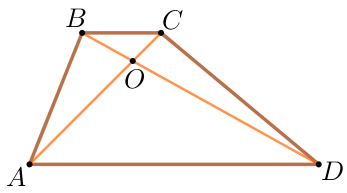 |
\(\displaystyle 1)\) тұжырымдағы "трапеция" сөзі "параллелограмм" деген сөзбен ауыстырылса, дұрыс болады.
Параллелограмм қасиеті
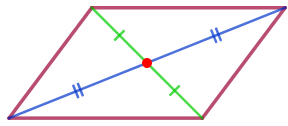 | Параллелограммның диагональдары қиылысу нүктесімен екіге бөлінеді. |
\(\displaystyle 2)\) Шеңбердің барлық диаметрлері тең.
Шеңбер берілген нүктеден бірдей қашықтықта орналасқан жазықтықтағы барлық нүктелердің жиыны. Шеңбер радиусы оның кез келген нүктесін центрмен қосатын түзу кесіндісі | 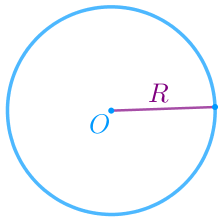 |
Шеңбердің барлық радиустары тең.
Диаметр- шеңбердің екі нүктесін қосатын және шеңбердің центрі арқылы өтетін кесінді, сонымен қатар осы кесіндінің ұзындығы. Диаметрі екі радиусқа тең. | 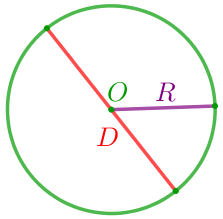 |
Барлық шеңбер диаметрлері тең.
\(\displaystyle 3)\) Үшбұрыштың бір бұрышы әрқашан \(\displaystyle 60\) градустан кіші.
Үшбұрыштың бұрыштарының қосындысы \(\displaystyle 180^{\circ}{\small}\\ \) тең. \(\displaystyle \color{red}{\alpha}+\color{green}{\beta}+\color{blue}{\gamma}=180^{\circ}\) |
Демек, үшбұрыштағы кіші бұрыш \(\displaystyle \leq 60^{\circ} {\small.}\) Сондықтан кез келген үшбұрышта \(\displaystyle 60\) градустан аспайтын бұрыш болады.
Жауабы: \(\displaystyle 23 {\small.}\)