Төмендегі тұжырымдардың қайсысы дұрыс?
\(\displaystyle 1)\) Тең қабырғалы үшбұрыштың барлық медианалары тең.
\(\displaystyle 2)\) Шеңберге іштей сызылған бұрыш сол доғаға тірелген сәйкес орталық бұрышқа тең.
\(\displaystyle 3)\) Кез келген ромбқа шеңберді жазуға болады.
Жауап ретінде таңдалған тұжырымдардың сандарын бос орынсыз, үтір немесе басқа қосымша таңбаларсыз жазыңыз
Әрбір тұжырымды қарастырайық:
\(\displaystyle 1)\) Тең қабырғалы үшбұрыштың барлық медианалары тең.
| Тең қабырғалы үшбұрыш - барлық қабырғаларының ұзындығы тең, барлық бұрыштары да тең және \(\displaystyle 60^{\circ} {\small}\) құрайтын үшбұрыш | 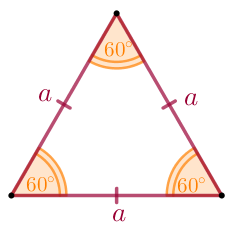 |
Тең қабырғалы үшбұрыштың қасиеті
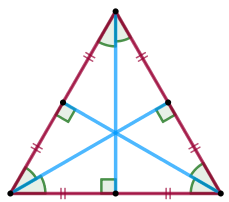 | Тең қабырғалы үшбұрышта әр қабырғаға жүргізілген медиана биссектриса және биіктік болып табылады және олар бір-біріне тең. |
\(\displaystyle 2)\) Шеңберге іштей сызылған бұрыш сол доғаға тірелген сәйкес орталық бұрышқа тең.
Орталық және сызылған бұрыш
| Іштей сызылған бұрыштың мәні сол доғаға тірелген орталық бұрыштың жарты шамасына тең. | 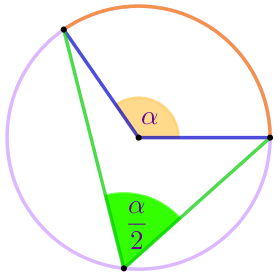 |
\(\displaystyle 3)\) Кез келген ромбқа шеңберді жазуға болады.
Сырттай сызылған төртбұрыштың белгісі
Егер төртбұрыштың қарама-қарсы қабырғаларының ұзындықтарының қосындылары тең болса, онда оған шеңберді іштей сызуға болады.
Егер \(\displaystyle \color{blue}{AB}+\color{blue}{CD}=\color{red}{BC}+\color{red}{AD}{\small,}\) онда \(\displaystyle ABCD\) – сырттай сызылған. |
| Ромб - барлық қабырғалары тең параллелограмм. | 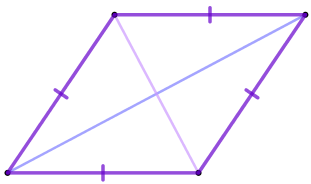 |
Демек, ромбтың қарама-қарсы қабырғаларының қосындылары тең. Яғни, бұл кез келген ромбқа шеңберді іштей сызуға болатынын білдіреді.
Жауабы: \(\displaystyle 13 {\small.}\)