Төмендегі тұжырымдардың қайсысы дұрыс?
\(\displaystyle 1)\) Барлық теңбүйірлі үшбұрыштар ұқсас.
\(\displaystyle 2)\) Диагональдары өзара перпендикуляр болатын тіктөртбұрыш болады.
\(\displaystyle 3)\) Тікбұрышты үшбұрыштың бұрыштарының қосындысы \(\displaystyle 90\) градусқа тең.
Жауап ретінде таңдалған тұжырымның нөмірін жазыңыз.
Әрбір тұжырымды қарастырайық:
\(\displaystyle 1)\) Барлық теңбүйірлі үшбұрыштар ұқсас.
Ұқсас үшбұрыштар
Егер екі үшбұрыштың бұрыштары сәйкесінше тең болса және бір үшбұрыштың қабырғалары екіншісінің ұқсас қабырғаларына пропорционалды болса, екі үшбұрыш ұқсас деп аталады.
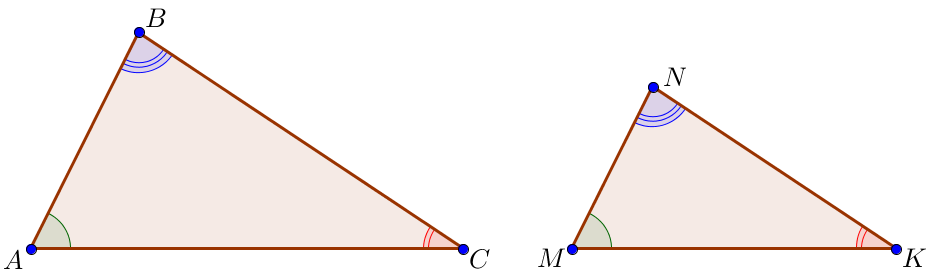
\(\displaystyle \triangle ABC \sim \triangle MNK\small: \)
\(\displaystyle \angle A = \angle M \small, \) \(\displaystyle \angle B = \angle N \small, \) \(\displaystyle \angle C = \angle K \small, \)
\(\displaystyle \frac{AB}{MN} = \frac{BC}{NK} = \frac{AC}{MK} \small. \)
Мысал.
Теңбүйірлі сүйір бұрышты және доғал бұрышты үшбұрыштар ұқсас емес.
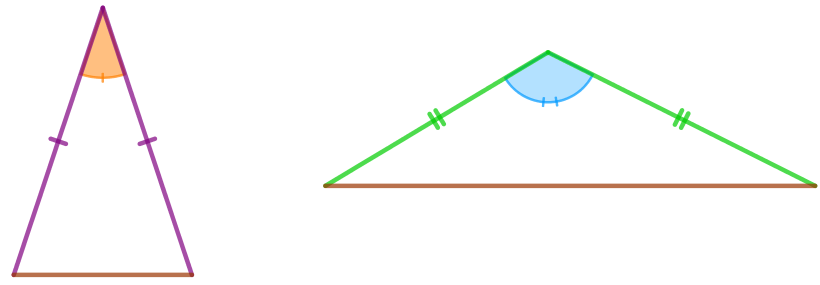
Сондықтан \(\displaystyle 1) \) тұжырымы қате.
\(\displaystyle 2)\) Диагональдары өзара перпендикуляр болатын тіктөртбұрыш болады.
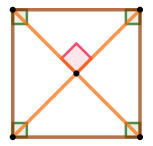 | Диагональдары өзара перпендикуляр болатын тіктөртбұрыш – бұл шаршы. |
\(\displaystyle 3)\) Тікбұрышты үшбұрыштың бұрыштарының қосындысы \(\displaystyle 90\) градусқа тең.
Үшбұрыштың бұрыштарының қосындысы ( \(\displaystyle 180^{\circ}{\small.}\)
| \(\displaystyle \color{red}{\alpha}+\color{green}{\beta}+\color{blue}{\gamma}=180^{\circ}\) |
Тұжырым дұрыс болуы үшін оны келесідей тұжырымдау керек:
Тік бұрышты үшбұрыштың сүйір бұрыштарының қосындысы \(\displaystyle 90\) градусқа тең.
Жауабы: \(\displaystyle 2 {\small.}\)