Параллелограммның диагоналы оның екі қабырғасымен \(\displaystyle 26^\circ\) және \(\displaystyle 34^\circ \small\) бұрыштарды құрайды.Параллелограммның ең үлкен бұрышын табыңыз. Жауабыңызды градуспен беріңіз.
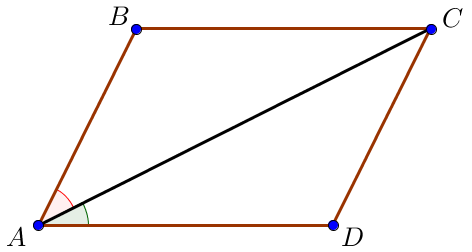
Диагональ \(\displaystyle AC\) қабырғасымен \(\displaystyle AD\) бұрышпен \(\displaystyle \color{green}{26^\circ } \small,\) және қабырғасымен \(\displaystyle AB\) – бұрыш \(\displaystyle \color{red}{34^\circ} \small\) болсын.
Содан кейін
\(\displaystyle \color{green}{\angle CAD} = \color{green}{26^\circ } {\small,}\) \(\displaystyle \color{red}{\angle BAC} = \color{red}{34^\circ }{\small.}\)
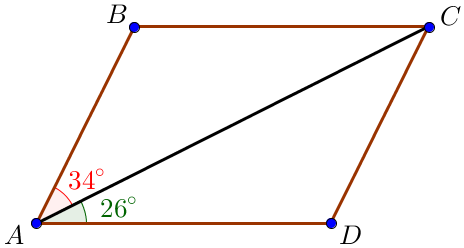
Параллелограмның бұрыштарын табыңыз.
\(\displaystyle \color{blue}{\angle BAD} = \color{red}{\angle BAC }+ \color{green}{\angle CAD} = \color{red}{34^\circ }+ \color{green}{26^\circ} = \color{blue}{60^\circ } \small.\)
Параллелограммның қасиеті бойынша бір қабырғасына іргелес жатқан бұрыштардың қосындысы \(\displaystyle 180^\circ \small\) тең, Демек,
\(\displaystyle \angle ADC + \color{blue}{\angle BAD }= 180^\circ \small.\)
Содан кейін
\(\displaystyle \angle ADC = 180^{\circ} - \color{blue}{\angle BAD }= 180^\circ - \color{blue}{60^\circ} = 120^\circ \small.\)
\(\displaystyle 120>60\) , болғандықтан, параллелограмның ең үлкен бұрышы \(\displaystyle 120^\circ \small.\)
Жауабы: \(\displaystyle 120 \small.\)