Один из углов параллелограмма равен \(\displaystyle 56^\circ \small.\) Найдите больший угол параллелограмма. Ответ дайте в градусах.

Пусть угол \(\displaystyle \color{green}{BAD}\) равен \(\displaystyle \color{green}{56^\circ}\small.\)
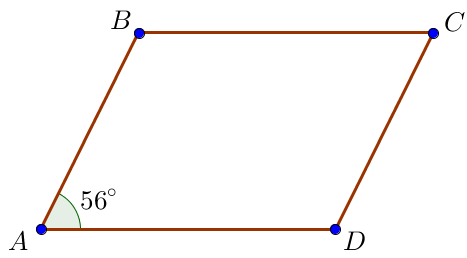
По свойству параллелограмма сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^\circ \small.\) Значит,
\(\displaystyle \angle ADC + \color{green}{\angle BAD }= 180^\circ\small.\)
Тогда
\(\displaystyle \angle ADC = 180^{\circ} - \color{green}{\angle BAD }= 180^\circ - \color{green}{56^\circ} = 124^\circ \small.\)
По свойству параллелограмма противоположные углы равны. Значит,
\(\displaystyle \angle BCD=\angle BAD=56^{\circ} \small,\)
\(\displaystyle \angle ABC=\angle ADC=124^{\circ} \small.\)
Так как \(\displaystyle 124>56\small,\) то наибольший угол параллелограмма составляет \(\displaystyle 124^\circ\small .\)
Ответ: \(\displaystyle 124 \small.\)