Колесо имеет \(\displaystyle 45\) спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
Изобразим колесо в виде окружности, спицы колеса – в виде радиусов этой окружности.
| рисунок | количество радиусов | количество секторов |
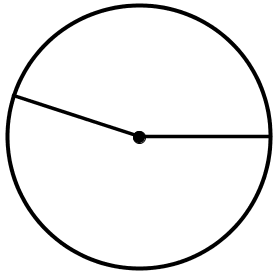 | \(\displaystyle \Large \color{blue}{2}\) | \(\displaystyle \Large \color{blue}{2}\) |
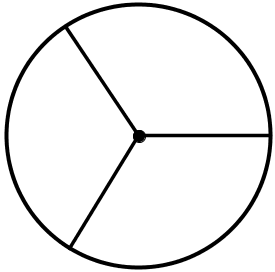 | \(\displaystyle \Large \color{blue}{3}\) | \(\displaystyle \Large \color{blue}{3}\) |
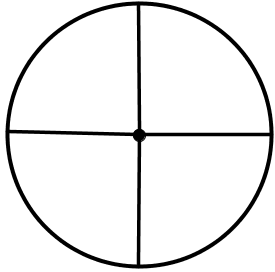 | \(\displaystyle \Large \color{blue}{4}\) | \(\displaystyle \Large \color{blue}{4}\) |
\(\displaystyle \Large {\vdots}\) | \(\displaystyle \Large \color{blue} {\vdots}\) | \(\displaystyle \Large \color{blue}{\vdots}\) |
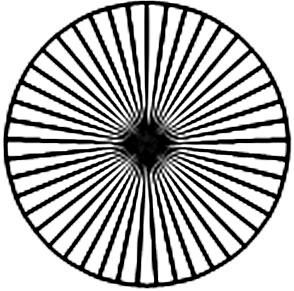 | \(\displaystyle \Large \color{blue}{n}\) | \(\displaystyle \Large \color{blue}{n}\) |
\(\displaystyle 45\) радиусов делят окружность на \(\displaystyle 45\) секторов. По условию задачи углы между соседними радиусами равны. Значит, углы секторов равны. Полный угол окружности составляет \(\displaystyle 360^{\circ} {\small.}\) Чтобы найти угол одного сектора, нужно \(\displaystyle 360^{\circ}\) разделить на \(\displaystyle 45\) частей. То есть \(\displaystyle 360^{\circ}:45=8^{\circ} \small.\) Угол между соседними спицами колеса равен \(\displaystyle 8^{\circ} {\small.} \) | 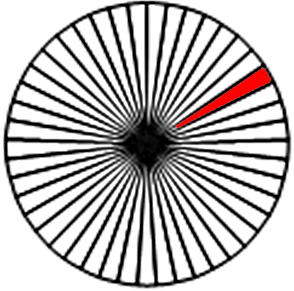 |
Ответ: \(\displaystyle 8 \small. \)