Дөңгелекте \(\displaystyle 45\) шабақ бар. Көрші шабақтар арасындағы бұрыштар тең. Көршілес екі шабақты құрайтын бұрыштың шамасын (градуспен) табыңыз.
Дөңгелекті шеңбер түрінде, дөңгелектің шабағын – осы шеңбердің радиусы түрінде бейнелейік.
| сурет | радиустар саны | секторлар саны |
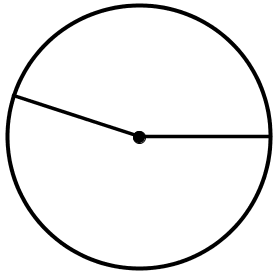 | \(\displaystyle \Large \color{blue}{2}\) | \(\displaystyle \Large \color{blue}{2}\) |
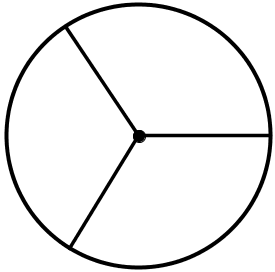 | \(\displaystyle \Large \color{blue}{3}\) | \(\displaystyle \Large \color{blue}{3}\) |
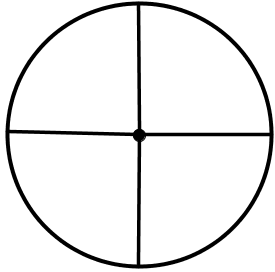 | \(\displaystyle \Large \color{blue}{4}\) | \(\displaystyle \Large \color{blue}{4}\) |
\(\displaystyle \Large {\vdots}\) | \(\displaystyle \Large \color{blue} {\vdots}\) | \(\displaystyle \Large \color{blue}{\vdots}\) |
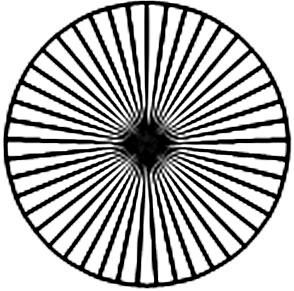 | \(\displaystyle \Large \color{blue}{n}\) | \(\displaystyle \Large \color{blue}{n}\) |
\(\displaystyle 45\) радиус шеңберді \(\displaystyle 45\) секторға бөледі. Есептің шарты бойынша көршілес радиустар арасындағы бұрыштар тең. Демек, секторлардың бұрыштары тең. Шеңбердің толық бұрышы \(\displaystyle 360^{\circ} {\small}\) құрайды. Бір сектордың бұрышын табу үшін \(\displaystyle 360^{\circ}\) \(\displaystyle 45\) бөлікке бөлу керек. Яғни \(\displaystyle 360^{\circ}:45=8^{\circ} \small.\) Дөңгелектің көршілес шабақтары арасындағы бұрыш \(\displaystyle 8^{\circ} {\small} \) тең. | 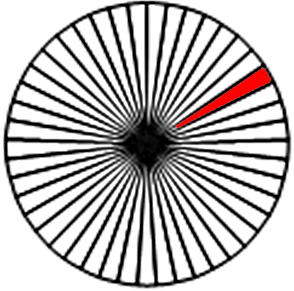 |
Жауабы: \(\displaystyle 8 \small. \)