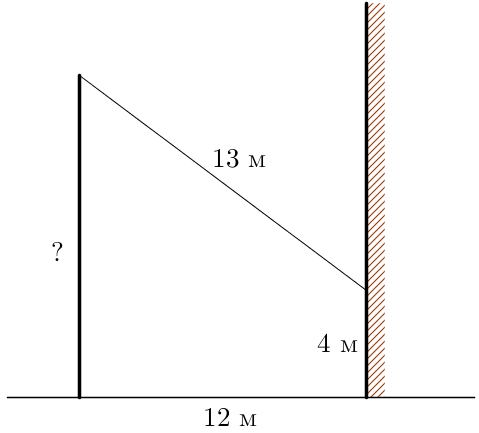
Бағанадан үйге ұзындығы \(\displaystyle 13\)м сым тартылған, ол жерден \(\displaystyle 4\)м биіктікте үйдің қабырғасына бекітілген (суретті қараңыз). Егер үйден бағанаға дейінгі қашықтық \(\displaystyle 12\)м болса, бағананың биіктігін табыңыз. Жауабын метрмен беріңіз.
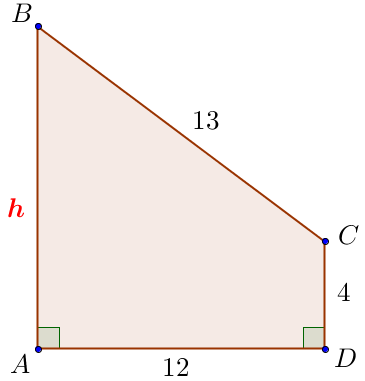
\(\displaystyle h\) – бағананың биіктігі болсын. Есепте ұсынылған құрылымды \(\displaystyle ABCD \small, \) тіктөртбұрышты трапеция түрінде бейнелейік ондағы: \(\displaystyle \angle A =90^{\circ} \small, \) \(\displaystyle \angle D =90^{\circ} \small, \) \(\displaystyle AB=h \small, \) \(\displaystyle AD=12 \small, \) \(\displaystyle CD=4 \small, \) \(\displaystyle BC=13 \small. \)
|  |
\(\displaystyle C\) нүктесінен \(\displaystyle AB\) қабырғасына \(\displaystyle CH \small \) перпендикулярын түсірейік
\(\displaystyle AHCD\) – тіктөртбұрыш. Тіктөртбұрыштың қарама-қарсы қабырғалары тең. Демек, \(\displaystyle HC=AD=12 \small, \) \(\displaystyle AH=CD=4\small. \) Сонда \(\displaystyle AB=BH+AH \small, \) \(\displaystyle h=BH+4\small. \) | 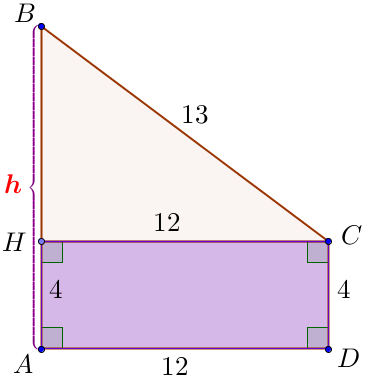 |
\(\displaystyle BH\small \) кесіндісінің ұзындығын табайық
\(\displaystyle BHC \small \) тікбұрышты үшбұрышын қарастырайық
Пифагор теоремасы бойынша \(\displaystyle BC^2=BH^2+HC^2 {\small,} \) \(\displaystyle BH^2=BC^2-HC^2 {\small,} \) \(\displaystyle BH^2=13^2-12^2=169-144=25{\small,} \) \(\displaystyle BH= \pm \sqrt{25}=\pm 5 \small. \) \(\displaystyle BH\) – \(\displaystyle BHC \small, \) тікбұрышты үшбұрышының катеті болғандықтан, онда \(\displaystyle BH>0 \small. \) Демек, \(\displaystyle BH=5\small. \) | 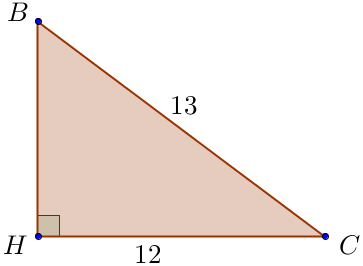 |
Бағананың биіктігін табайық:
\(\displaystyle h=BH+4\small, \)
\(\displaystyle h=5+4=9 \small. \)
Бағананың биіктігі \(\displaystyle 9\) метрге тең.
Жауабы: \(\displaystyle 9 \small. \)