Найдите площадь фигуры, если нанесена сетка из единичных квадратов.
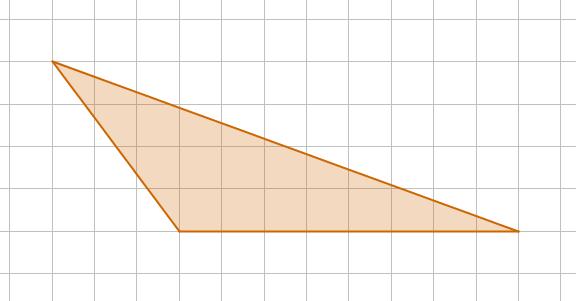
Проведем высоту \(\displaystyle DH\) к основанию \(\displaystyle EF{\small : }\)

По рисунку:
- длина основания \(\displaystyle EF\) равна \(\displaystyle 8{\small , }\)
- длина высоты \(\displaystyle DH\) к основанию равна \(\displaystyle 4{\small . }\)
Так как площадь треугольника равна половине произведения основания на высоту, то площадь данного треугольника равна
\(\displaystyle \frac{1}{2}\cdot 8 \cdot 4=16{\small . }\)
Ответ: \(\displaystyle 16{\small . }\)
По определению высота треугольника – это перпендикуляр, опущенный из вершины треугольника к противоположной стороне или к продолжению противоположной стороны треугольника.
В данной задаче высота \(\displaystyle DH\) проведена к продолжению стороны \(\displaystyle EF\small.\)