Егер бірлік квадраттары бар тор қолданылса, ішкі шеңбердің ауданын есепке алмай, үлкен шеңбердің ауданын \(\displaystyle S\) табтабыңыз. Жауабына \(\displaystyle \frac{S}{\pi}\small \) жазыңыз.
Ішкі шеңбер радиусы \(\displaystyle r=2 \small \) тең. Ішкі шеңбердің ауданы \(\displaystyle S_1=\pi \cdot r^2=\pi \cdot 2^2=4 \pi \small \\ \) тең. Үлкен шеңбердің ауданы \(\displaystyle R=5 \small \) тең. Үлкен шеңбердің ауданы \(\displaystyle S_2=\pi \cdot R^2=\pi \cdot 5^2=25 \pi \small\\ \) тең. | 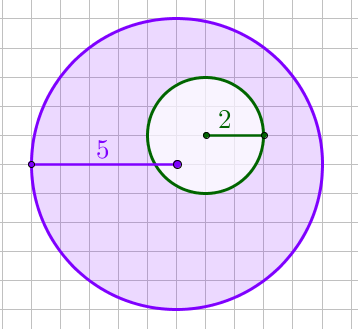 |
Ізделініп отырған аймақтың ауданы үлкен және ішкі шеңберлердің аудандарының айырмасына тең:
\(\displaystyle S=S_2-S_1=25\pi-4\pi=21\pi{\small .}\)
Сонда
\(\displaystyle \frac{S}{\pi}=\frac{21\pi}{\pi}=21 \small. \)
Жауабы: \(\displaystyle 21 {\small .}\)