Основания равнобедренной трапеции равны \(\displaystyle 7\) и \(\displaystyle 13 \small,\) а её площадь равна \(\displaystyle 40 \small.\) Найдите периметр трапеции.
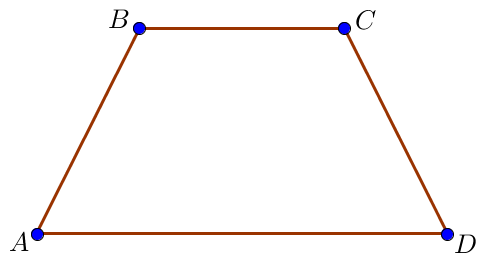
Пусть \(\displaystyle AD=13\) и \(\displaystyle BC=7\) – основания, \(\displaystyle AB=CD\) – боковые стороны, Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, \(\displaystyle BH K C \) – прямоугольник. Тогда \(\displaystyle H K =BC=7 \small.\) | 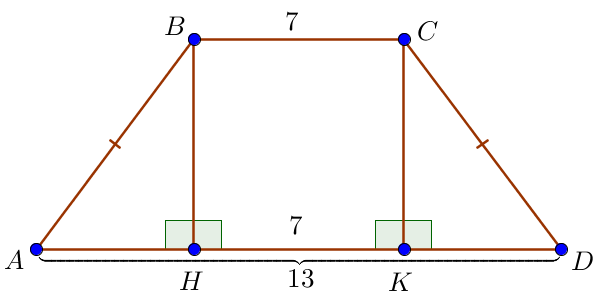 |
Прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCK\) равны по гипотенузе \(\displaystyle AB=CD\) Значит, \(\displaystyle AH=DK\) и \(\displaystyle AH=DK=\frac{AD-BC}{2}=\) \(\displaystyle =\frac{13-7}{2}=\frac{6}{2}=3 \small.\) | 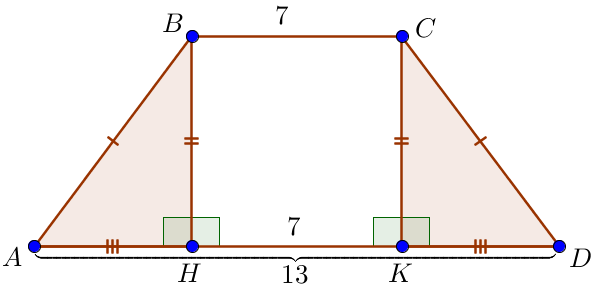 |
Найдем высоту \(\displaystyle BH\) трапеции через площадь. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту,
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH \small,\)
то
\(\displaystyle 40=\frac{13+7}{2}\cdot BH \small,\)
\(\displaystyle 40=10\cdot BH \small,\)
\(\displaystyle BH=\frac{40}{10}=4 \small.\)
Боковую сторону \(\displaystyle AB\) трапеции найдем из прямоугольного треугольника \(\displaystyle ABH \small.\)
По теореме Пифагора \(\displaystyle AB^2=BH^2+AH^2 \small.\) Значит, \(\displaystyle AB^2=4^2+3^2=16+9=25=5^2 \small.\) Поскольку длина отрезка положительна, то \(\displaystyle AB=5 \small.\) | 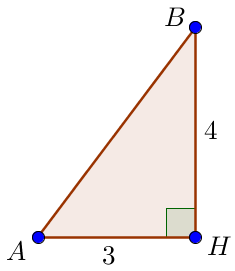 |
Периметр трапеции равен сумме всех ее сторон:
\(\displaystyle P_{ABCD}=AB+BC+CD+DA=5+7+5+13=30 \small.\)
Ответ: \(\displaystyle 30 {\small .}\)