Теңбүйірлі трапецияның табандары \(\displaystyle 7\) және \(\displaystyle 13,\) ауданы \(\displaystyle 40.\) Трапецияның периметрін табыңыз.
\(\displaystyle AD=13\) және \(\displaystyle BC=7\) – табандары, \(\displaystyle AB=CD\) – бүйір қабырғалары болсын, Трапецияның табандары параллель және трапецияның биіктіктері табандарына перпендикуляр болғандықтан , \(\displaystyle BH K C \) – тіктөртбұрыш. Сонда \(\displaystyle H K =BC=7 \small.\) | 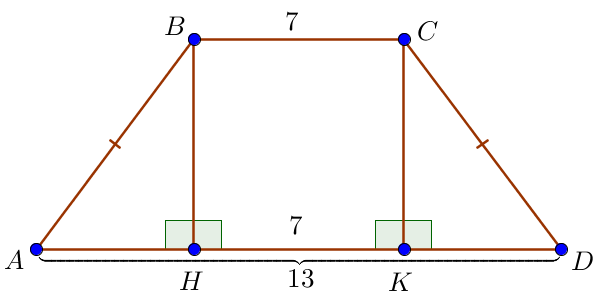 |
\(\displaystyle ABH\) және \(\displaystyle DCK\) тікбұрышты үшбұрыштары гипотенузалары \(\displaystyle AB=CD\) Демек, \(\displaystyle AH=DK\) және \(\displaystyle AH=DK=\frac{AD-BC}{2}=\) \(\displaystyle =\frac{13-7}{2}=\frac{6}{2}=3 \small.\) | 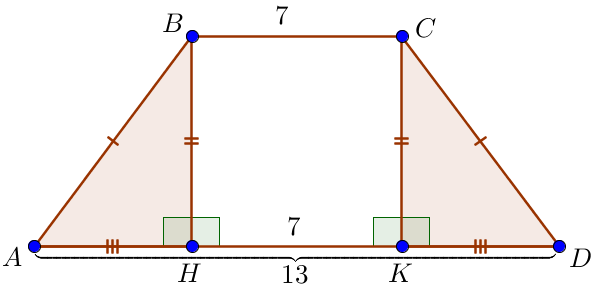 |
Ауданы арқылы трапецияның \(\displaystyle BH\) биіктігін табамыз. Трапецияның ауданы табандарының қосындысының жартысы мен биіктігінің көбейтіндісіне тең болғандықтан
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH \small,\)
онда
\(\displaystyle 40=\frac{13+7}{2}\cdot BH \small,\)
\(\displaystyle 40=10\cdot BH \small,\)
\(\displaystyle BH=\frac{40}{10}=4 \small.\)
\(\displaystyle ABH \small\) тікбұрышты үшбұрышынан трапецияның \(\displaystyle AB\) бүйір қабырғасын табамыз
Пифагор теоремасы бойынша \(\displaystyle AB^2=BH^2+AH^2 \small.\) білдіреді, \(\displaystyle AB^2=4^2+3^2=16+9=25=5^2 \small.\) Кесіндінің ұзындығы оң болғандықтан \(\displaystyle AB=5 \small.\) | 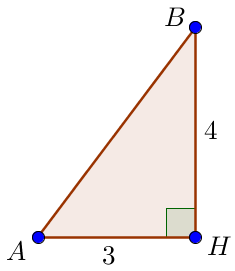 |
Трапецияның периметрі оның барлық қабырғаларының қосындысына тең:
\(\displaystyle P_{ABCD}=AB+BC+CD+DA=5+7+5+13=30 \small.\)
Жауабы: \(\displaystyle 30 {\small .}\)