Тік бұрышты трапецияның табандары \(\displaystyle 10 \) және \(\displaystyle 4 .\) Оның ауданы \(\displaystyle 14\sqrt{3}\small.\) Осы трапецияның сүйір бұрышын табыңыз. Жауабыңызды градуспен көрсетіңіз.
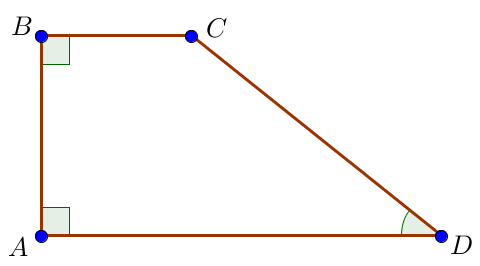
\(\displaystyle ABCD\) – тікбұрышты трапециясында \(\displaystyle A\) және \(\displaystyle B\) бұрыштары тік және \(\displaystyle C\small\) бұрышы доғал бұрыш болсын, онда оның табандары \(\displaystyle BC=4\) және \(\displaystyle AD=10\small,\) \(\displaystyle \\ \)үлкен бүйір қабырғасы \(\displaystyle CD\small.\) \(\displaystyle CH\small\) биіктігін түсіреміз \(\displaystyle ABCH\) төртбұрышының барлық бұрыштары тік болғандықтан, ол тіктөртбұрыш. Сонымен \(\displaystyle AH=BC=4\small.\) Онда \(\displaystyle HD=AD-AH=10-4=6\small.\) | 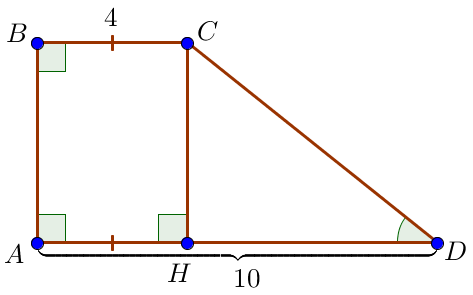 |
Трапецияның ауданы табандарының қосындысының жартысының биіктігіне көбейтіндісіне тең болғандықтан,
\(\displaystyle {S_{трап}} = \frac{{AD}+{BC}}{2}\cdot {CH} {\small ,}\)
онда
\(\displaystyle 14\sqrt{3} = \frac{{10}+{4}}{2}\cdot {CH} {\small ,}\\ \)
\(\displaystyle 14\sqrt{3} = 7 \cdot {CH} {\small ,}\)
осыдан
\(\displaystyle {CH}=\frac{14\sqrt{3}}{7}=2\sqrt{3} {\small .}\)
\(\displaystyle CDH\) тікбұрышты үшбұрышынан трапецияның \(\displaystyle CHD\small\) сүйір бұрышын табамыз
Бізге \(\displaystyle CH=2\sqrt{3}\) және \(\displaystyle HD=6\small\) катеттері белгілі Пифагор теоремасы бойынша \(\displaystyle \begin{aligned} CD^2&=CH^2+DH^2=\\&=(2\sqrt{3})^2+6^2=12+36=48\small.\end{aligned}\) Кесіндінің ұзындығы оң болғандықтан, онда \(\displaystyle CD=\sqrt{48}=4\sqrt{3}\small.\) \(\displaystyle CD\) гипотенузасы \(\displaystyle CH\small,\) катетінен екі есе үлкен болатындықтан \(\displaystyle CH\) катетіне қарсы \(\displaystyle 30^{\circ}\small\) бұрыш жатады, \(\displaystyle \angle CDH=30^{\circ}\small.\) | 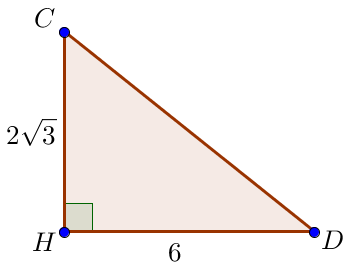 |
Жауабы: \(\displaystyle 30^{\circ}\small.\)