Трапецияның ауданы \(\displaystyle 14 , \) диагональдарының бірі \(\displaystyle 7 \small,\), диагональдардың арасындағы бұрыштың синусы \(\displaystyle 0{,}2 \small.\) Трапецияның екінші диагоналін табыңыз.
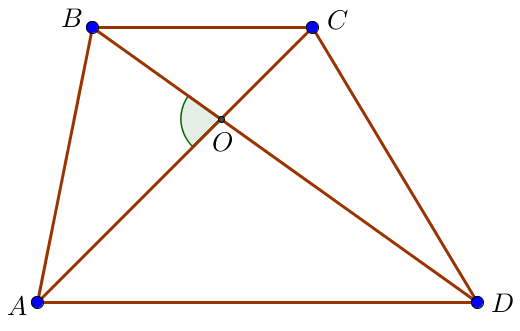
Трапецияның ауданын есептейтін формуланы қолданайық:
\(\displaystyle S_{тр}=\frac{d_1 \cdot d_2}{2} \cdot \sin \varphi \small,\)
мұндағы \(\displaystyle d_1\) және \(\displaystyle d_2\) – трапецияның диагональдары, \(\displaystyle \varphi \) – трапеция диагональдарының арасындағы бұрыш..
Бұл жағдайда \(\displaystyle d_1=7 \small,\) \(\displaystyle \sin \varphi =0{,}2\) және \(\displaystyle S_{тр}=14 {\small : } \)
\(\displaystyle {14} = \frac{7 \cdot d_2}{2} \cdot 0{,}2 {\small ,}\)
осыдан
\(\displaystyle {14} = 0{,}7 \cdot d_2 {\small ,}\)
\(\displaystyle d_2 = \frac{14}{0{,}7} = 20{\small .}\)
Жауабы: \(\displaystyle 20{\small .}\)