Высота равнобедренного треугольника равна \(\displaystyle 4 \small,\) основание равно \(\displaystyle 6 \small.\) Найдите радиус вписанной окружности.
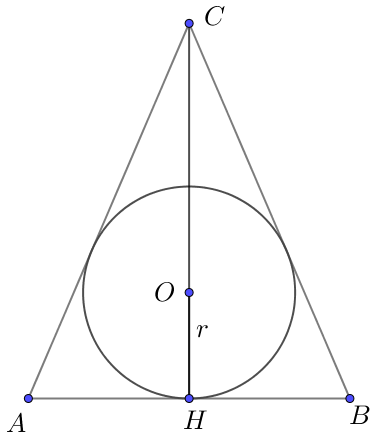
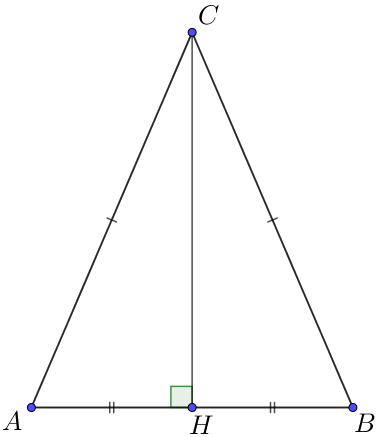 | Пусть \(\displaystyle ABC\) – равнобедренный треугольник с высотой \(\displaystyle CH=4\) и основанием \(\displaystyle AB=6 \small.\) По свойству равнобедренного треугольника, высота \(\displaystyle CH\) является и медианой, \(\displaystyle AH=BH=\frac{1}{2} \cdot AB=3 \small.\) Из прямоугольного треугольника \(\displaystyle ACH\) по теореме Пифагора получаем: \(\displaystyle AC^2=AH^2+CH^2 \small,\) тогда \(\displaystyle AC^2=3^2+4^2=9+16=25 \small,\) \(\displaystyle AC=5 \small.\) |
Значит,
\(\displaystyle S=\frac{1}{2} \cdot AB\cdot CH=\frac{1}{2}\cdot 6\cdot 4=12 \small.\)
Периметр треугольника равен
\(\displaystyle P=AB+BC+CA=6+5+5=16 \small,\)
отсюда полупериметр равен
\(\displaystyle p=\frac{1}{2} \cdot P=8 \small.\)
По формуле
Площадь треугольника через радиус вписанной окружности
\(\displaystyle S=pr \small,\)
\(\displaystyle p=\frac{a+b+c}{2}\) – полупериметр,
\(\displaystyle r\) – радиус вписанной окружности.
получаем:
\(\displaystyle r=\frac{S}{p}=\frac{12}{8}=1{,}5 \small.\)
Ответ: \(\displaystyle 1{,}5 {\small .}\)