Теңбүйірлі үшбұрыштың биіктігі \(\displaystyle 4 ,\) табаны \(\displaystyle 6 \) тең. Іштей сызылған шеңбердің радиусын табыңыз.
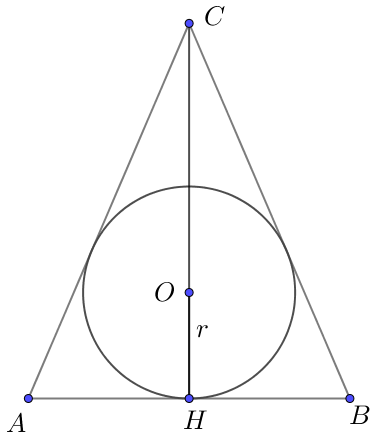
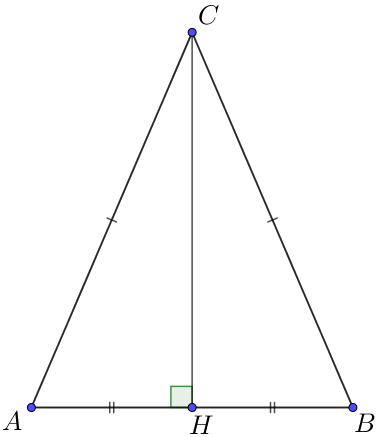 | \(\displaystyle ABC\) – биіктігі \(\displaystyle CH=4\) және табаны \(\displaystyle AB=6 \small\) болатын теңбүйірлі үшбұрыш болсын. Теңбүйірлі үшбұрыштың қасиеті бойынша \(\displaystyle CH\) биіктігі медиана да болып табылады, \(\displaystyle AH=BH=\frac{1}{2} \cdot AB=3 \small.\) \(\displaystyle ACH\) тікбұрышты үшбұрыштан Пифагор теоремасы бойынша төмендегіні аламыз: \(\displaystyle AC^2=AH^2+CH^2 \small,\) сонда \(\displaystyle AC^2=3^2+4^2=9+16=25 \small,\) \(\displaystyle AC=5 \small.\) |
Яғни,
\(\displaystyle S=\frac{1}{2} \cdot AB\cdot CH=\frac{1}{2}\cdot 6\cdot 4=12 \small.\)
Үшбұрыштың периметрі келесіге тең
\(\displaystyle P=AB+BC+CA=6+5+5=16 \small,\)
осыдан жарты периметр
\(\displaystyle p=\frac{1}{2} \cdot P=8 \small.\)
Формула бойынша
Іштей сызылған шеңбердің радиусы арқылы үшбұрыштың ауданы
\(\displaystyle S=pr \small,\)
\(\displaystyle p=\frac{a+b+c}{2}\) – жарты периметр,
\(\displaystyle r\) – іштей сызылған шеңбердің радиусы.
төмендегіні аламыз:
\(\displaystyle r=\frac{S}{p}=\frac{12}{8}=1{,}5 \small.\)
Жауабы: \(\displaystyle 1{,}5 {\small .}\)