Тікбұрышты үшбұрыштың катеттері \(\displaystyle 6\) және \(\displaystyle 8 \) тең. Іштей сызылған шеңбердің радиусын табыңыз.
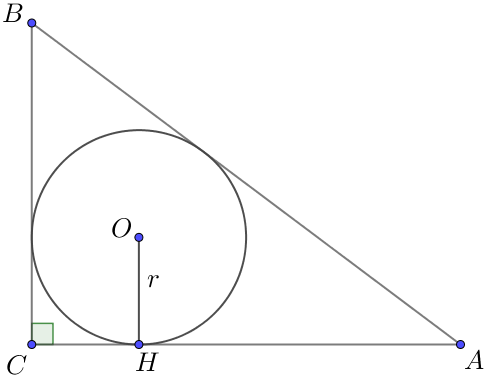
\(\displaystyle AC=8\) және \(\displaystyle BC=6\) – тікбұрышты \(\displaystyle ABC \small\) үшбұрышының катеттері болсын
\(\displaystyle ABC\) тікбұрышты үшбұрышынан Пифагор теоремасы бойынша
\(\displaystyle AB^2=BC^2+AC^2 \small.\)
Сонда
\(\displaystyle AB^2=6^2+8^2=36+64=100 \small.\)
Кесіндінің ұзындығы оң болғандықтан, онда \(\displaystyle AB=10 \small.\)
Тікбұрышты \(\displaystyle ABC\) үшбұрышында аудан мен жарты периметрді табамыз:
\(\displaystyle S=\frac{1}{2} \cdot AC \cdot BC= \frac{1}{2} \cdot 8 \cdot 6=24 \small, \\ \)
\(\displaystyle p=\frac{AB+BC+AC}{2}=\frac{10+6+8}{2}=12. \small\)
Формула бойынша
Іштей сызылған шеңбердің радиусы арқылы үшбұрыштың ауданы
\(\displaystyle S=pr\)
төмендегіні аламыз:
\(\displaystyle 24={12}\cdot r{\small ,} \)
\(\displaystyle r=2{\small .} \)
Жауабы: \(\displaystyle 2 {\small .}\)