Дұрыс үшбұрыштың қабырғасы \(\displaystyle \sqrt{3} \small\)тең. Осы үшбұрышқа іштей сызылған шеңбердің радиусын табыңыз.
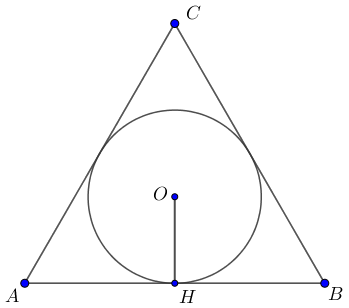
Дұрыс \(\displaystyle ABC\) үшбұрышының \(\displaystyle CH\) биіктігін жүргізейік .
\(\displaystyle O\) нүктесі - іштей сызылған шеңбердің центрі болсын.
Үшбұрышқа іштей сызылған шеңбердің центрі – биссектрисалардың қиылысу нүктесі.
Дұрыс үшбұрыштың биссектрисалары сондай ақ биіктіктер болып табылады. Яғни, \(\displaystyle O\) нүктесі \(\displaystyle CH \small\) биіктігінде жатыр. \(\displaystyle OH\) кесіндісі үшбұрыштың табанына перпендикуляр болғандықтан, ол шеңбердің радиусы болып табылады. |
Тең қабырғалы үшбұрыштың \(\displaystyle CH\) биіктігі оның медианасы да болғандықтан, онда
\(\displaystyle AH=\frac{1}{2} \cdot AB=\frac{\sqrt{3}}{2} \small.\)
Тікбұрышты \(\displaystyle ACH \small\) үшбұрышынан \(\displaystyle CH\) кесіндінің ұзындығын табамыз
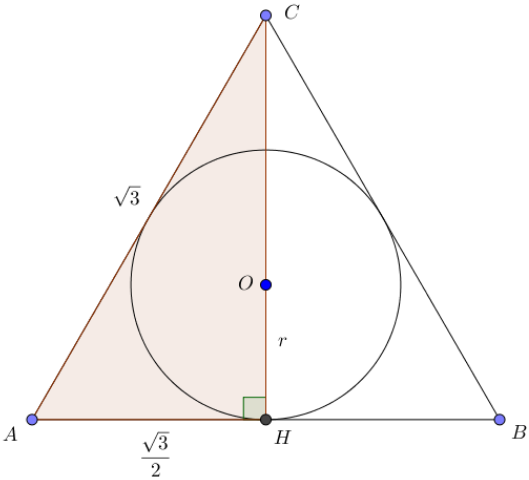 | Пифагор теоремасы бойынша \(\displaystyle AC^2=AH^2+CH^2 \small.\) Сонда \(\displaystyle CH^2=AC^2-AH^2 \small,\) \(\displaystyle CH^2=(\sqrt{3})^2-\left( \frac{\sqrt{3}}{2}\right)^2=3-\frac{3}{4}=\frac{9}{4}\small.\) Кесіндінің ұзындығы оң болғандықтан, онда \(\displaystyle CH=\frac{3}{2} \small.\) |
Дұрыс үшбұрыштың биіктігі сондай-ақ медианалар болып табылады, яғни \(\displaystyle O\) – нүктесі – медианалардың қиылысу нүктесі..
Сонда \(\displaystyle O\) нүктесі \(\displaystyle CH\) медианасын \(\displaystyle C \small\) төбесінен есептей отырып \(\displaystyle 2:1 \small,\) қатынасында бөледі
Демек,
\(\displaystyle r=\frac{1}{3} \cdot CH=\frac{1}{3} \cdot \frac{3}{2}=\frac{1}{2}=0{,}5 \small.\)
Жауабы: \(\displaystyle 0{,}5 {\small .}\)