Тең қабырғалы трапецияның табанындағы екі бұрыштың қосындысы \(\displaystyle 136^\circ\small.\) Трапецияның ең үлкен бұрышының мәнін табыңыз. Жауабыңызды градуспен беріңіз.

\(\displaystyle AD\) және \(\displaystyle BC\small\) - \(\displaystyle ABCD\) тең қабырғалы трапецияның табандары.
Тең қабырғалы трапеция қасиетін қолданамыз.
Тең қабырғалы трапецияның қасиеті
Тең қабырғалы трапецияның табанындағы бұрыштары тең.
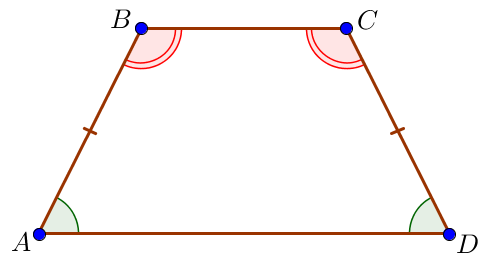
Сонда \(\displaystyle \angle A=\angle D\small,\) \(\displaystyle \angle B=\angle C\small.\)
Өйткені \(\displaystyle \angle B=\angle C>90^{\circ}\small,\) онда
\(\displaystyle \angle B + \angle C>180^{\circ}>136^{\circ}\small.\)
Сондықтан, біз негіздегі бұрыштар туралы айтып отырған жағдайда \(\displaystyle AD{\small: }\)
\(\displaystyle \angle A+\angle D=136^{\circ}\small.\)
Біз алып жатырмыз:
\(\displaystyle 2\angle A=136^{\circ}\small,\)
\(\displaystyle \angle A=68^{\circ}\small.\)
Трапецияның бүйір жағындағы бұрыштардың қосындысы \(\displaystyle 180^{\circ}\small,\) болғандықтан трапецияның ең үлкен бұрышы
\(\displaystyle \angle B=180^{\circ}-\angle A=180^{\circ}-68^{\circ}=112^{\circ}\small.\)
Жауабы: \(\displaystyle 112 \small.\)