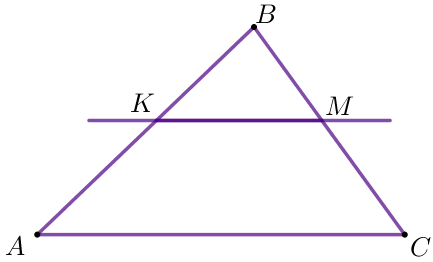
Үшбұрыштың \(\displaystyle ABC\) қабырғасына \(\displaystyle АС\) параллель түзу \(\displaystyle АВ\) және \(\displaystyle ВС\) қабырғаларын сәйкесінше \(\displaystyle K\) және \(\displaystyle M\) нүктелерінде қиып өтеді. \(\displaystyle BK:KA=3:4 {\small,}\) \(\displaystyle KM=18 {\small}\) болса \(\displaystyle АС \) табыңыз.
\(\displaystyle KM \parallel AC {\small,} \) \(\displaystyle AB\) – қима болғандықтан \(\displaystyle \angle BKM= \angle BAC\) \(\displaystyle (\)сәйкес бұрыштар\(\displaystyle ){\small.}\)
 | Үшбұрыштарды \(\displaystyle KBM\) және \(\displaystyle ABC {\small} \\ \) қарастырайық
|
Демек,
\(\displaystyle \frac{KM}{AC}= \frac{BK}{BA} {\small.} \\ \)
Алынған теңдіктен пропорционалды түрде \(\displaystyle AC {\small}\) өрнектейміз
\(\displaystyle AC= \frac{BA}{BK} \cdot KM{\small.} \)
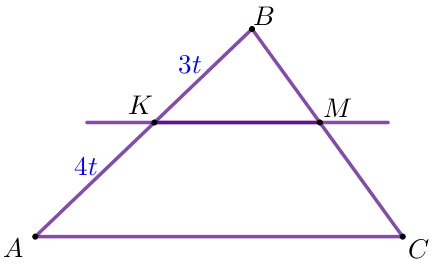 | Шарты бойынша \(\displaystyle BK:KA=3:4 {\small.} \\ \) Онда \(\displaystyle BK=3t {\small,}\) \(\displaystyle KA=4t {\small,}\) болсын \(\displaystyle \\ \frac{BA}{BK}= \frac{BK+KA}{BK}=\frac{3t+4t}{3t}=\frac{7}{3} {\small.} \)
|
Біз алып жатырмыз
\(\displaystyle AC= \frac{BA}{BK} \cdot KM=\frac{7}{3} \cdot 18=42{\small.} \)
Жауабы: \(\displaystyle 42 {\small.}\)