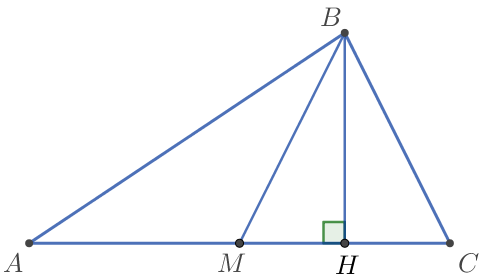
В треугольнике \(\displaystyle ABC\) сторона \(\displaystyle AC=79 {\small,}\) \(\displaystyle BM\) – медиана, \(\displaystyle BH\) – высота, \(\displaystyle BC=BM {\small.}\)
Найдите длину отрезка \(\displaystyle AH {\small.}\)
Длина отрезка \(\displaystyle AH\) равна: \(\displaystyle AH=AM+MH {\small.}\) Найдём длины отрезков \(\displaystyle AM\) и \(\displaystyle MH {\small.}\) По условию сторона \(\displaystyle AC=79\) и \(\displaystyle BM\) – медиана треугольника \(\displaystyle ABC {\small.}\) Тогда \(\displaystyle AM=MC= \frac{1}{2} \cdot AC= \frac{1}{2} \cdot 79=39{,}5{\small.}\) | 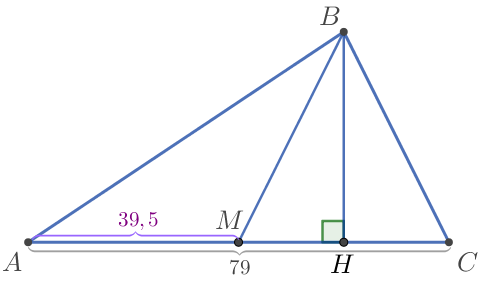 |
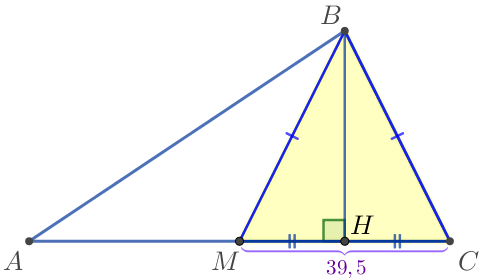 | Рассмотрим треугольник \(\displaystyle MBC {\small:}\)
Так как в равнобедренном треугольнике высота, проведённая к основанию, является и медианой, то \(\displaystyle MH=HC= \frac{1}{2} \cdot MC= \frac{1}{2} \cdot 39{,}5=19{,}75{\small.}\) |
Получаем: \(\displaystyle AH=AM+MH {\small,}\) \(\displaystyle AH=39{,}5+19{,}75=59{,}25{\small.}\) | 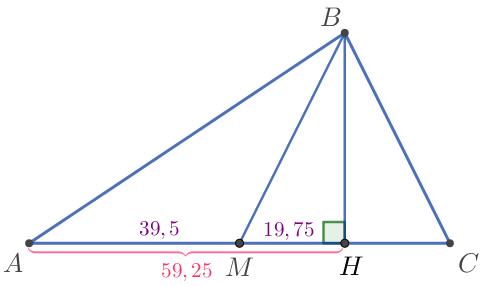 |
Ответ: \(\displaystyle 59{,}25 {\small.}\)