Skip to main content

Теориясы: 03 Биссектриса, медиана, биіктік

Тапсырма

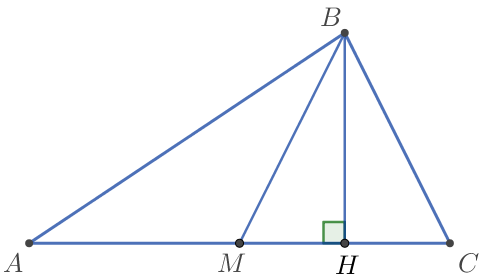
Үшбұрышта \(\displaystyle ABC\) жағы \(\displaystyle AC=79 {\small,}\) \(\displaystyle BM\) – медиана, \(\displaystyle BH\) – биіктік, \(\displaystyle BC=BM {\small.}\)

Кесіндінің \(\displaystyle AH {\small}\) ұзындығын табыңыз

Шешім

 \(\displaystyle AH\) кесіндінің ұзындығы тең: 

\(\displaystyle AH=AM+MH {\small.}\)

 \(\displaystyle AM\) және \(\displaystyle MH {\small}\) кесінділерінің ұзындығын табамыз

Шарт бойынша    \(\displaystyle AC=79\) және \(\displaystyle BM\) –жағы \(\displaystyle ABC {\small}\) үшбұрыш медианасы. Онда

\(\displaystyle AM=MC= \frac{1}{2} \cdot AC= \frac{1}{2} \cdot 79=39{,}5{\small.}\)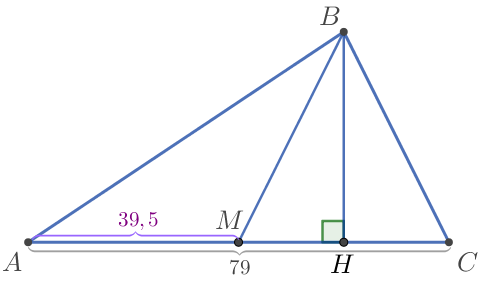

 

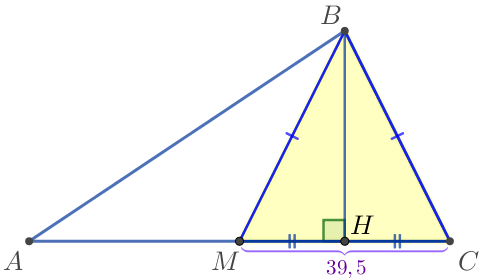Үшбұрышты \(\displaystyle MBC {\small:}\) қарастырамыз

  • \(\displaystyle MC=39{,}5 {\small;}\)
  • \(\displaystyle BC=BM\) (Шарт бойынша);
  • \(\displaystyle BH\) – биіктік (Шарт бойынша).

Сонымен теңбүйірлі үшбұрышта табанға тартылған биіктік медиана болып табылады, содан кейін

\(\displaystyle MH=HC= \frac{1}{2} \cdot MC= \frac{1}{2} \cdot 39{,}5=19{,}75{\small.}\)

 

Аламыз:

\(\displaystyle AH=AM+MH {\small,}\)

\(\displaystyle AH=39{,}5+19{,}75=59{,}25{\small.}\)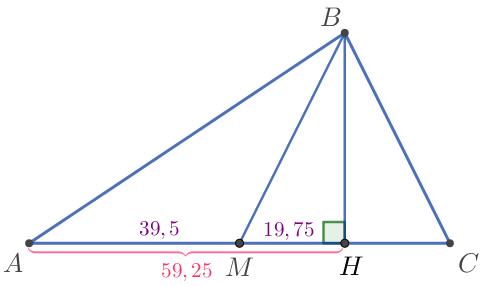

Жауап: \(\displaystyle 59{,}25 {\small.}\)