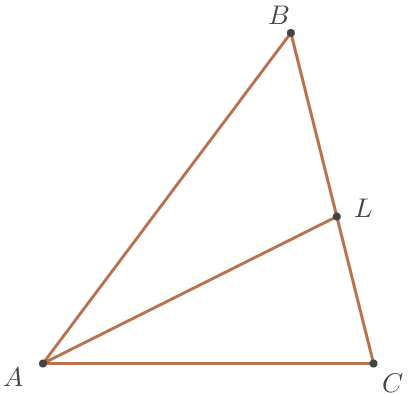
Үшбұрышта \(\displaystyle ABC\) биссектриса \(\displaystyle AL{\small,}\) бұрыш \(\displaystyle ALC\) \(\displaystyle 76^{\circ} {\small,}\) тең \(\displaystyle ABC\) бұрыш \(\displaystyle 47^{\circ}{\small}\) тең. Бұрышты \(\displaystyle ACB{\small}\) табыңыз. Жауабын градуспен беріңіз.
Егер \(\displaystyle \angle ACB=\color{red}{x} {\small.}\) Шарт бойынша \(\displaystyle \angle ALC=76^{\circ} \) және \(\displaystyle \angle ABC=47^{\circ} {\small.}\) Сонымен \(\displaystyle AL\) – бұрыш биссектрисасы \(\displaystyle BAC {\small,}\) онда \(\displaystyle \angle BAL=\angle CAL=\alpha {\small.}\) Сонымен үшбұрыштың ішкі бұрыштарының қосындысы \(\displaystyle 180^{\circ} {\small,}\) онда үшбұрышта \(\displaystyle ALC \) угол \(\displaystyle \color{red}x \) тең \(\displaystyle \color{red}x= 180^{\circ}-76^{\circ}- \alpha {\small,}\) \(\displaystyle \color{red}x= 104^{\circ}- \alpha {\small.}\) | 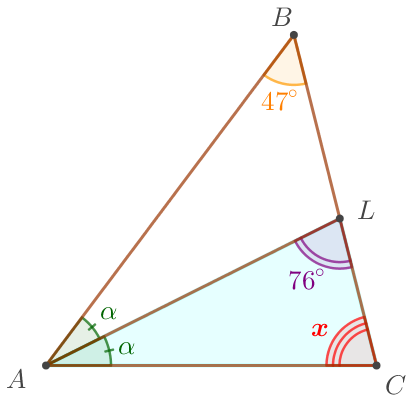 |
Бұрышты \(\displaystyle \alpha \) үшбұрыштан \(\displaystyle ABL {\small}\) табамыз
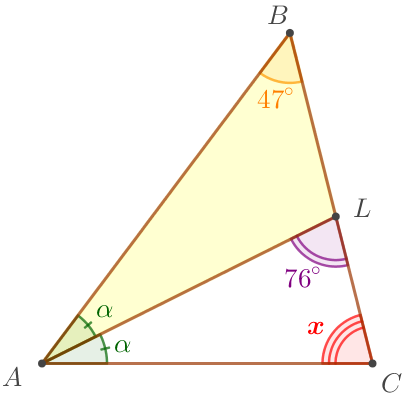 | \(\displaystyle \angle ALC \) – \(\displaystyle ABL {\small}\) үшбұрыштың сыртқы бұрышы. Сонымен үшбұрыштың сыртқы бұрышы оған іргелес емес екі бұрыштың қосындысына тең, содан кейін \(\displaystyle 76^{\circ}=\alpha+47^{\circ} {\small.}\) Онда \(\displaystyle \alpha=76^{\circ}-47^{\circ} = 29^{\circ}{\small.}\) Аламыз \(\displaystyle \color{red}x= 104^{\circ}-29^{\circ}=75^{\circ} {\small.}\) |
Жауап: \(\displaystyle 75 {\small.} \)