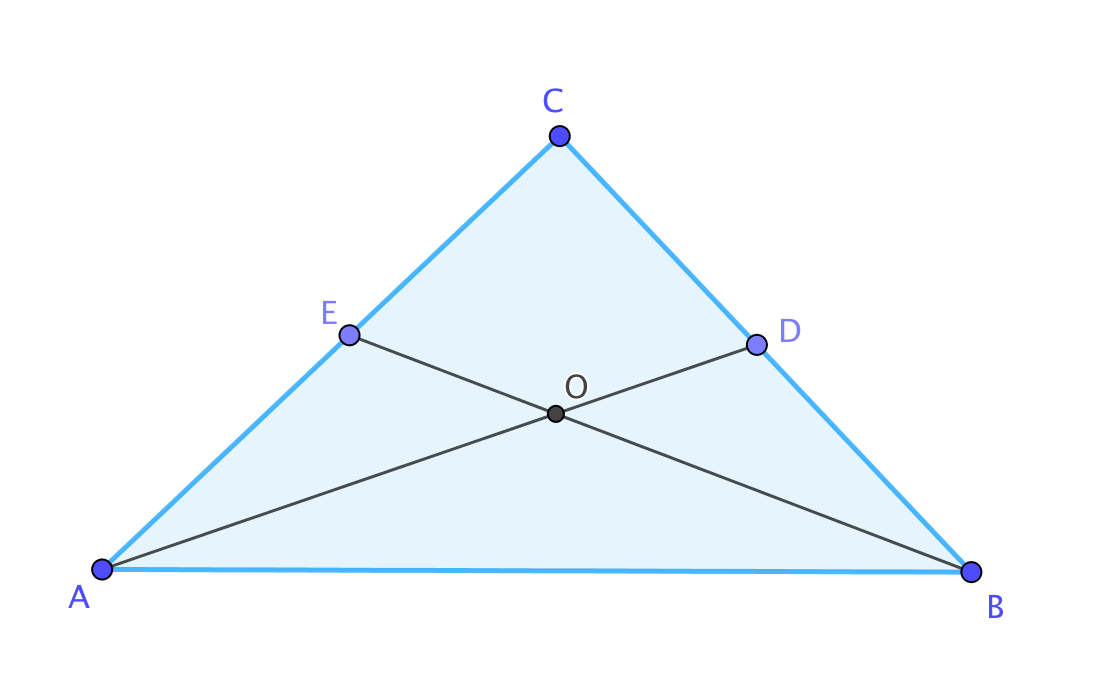
\(\displaystyle ABC\) үшбұрышта \(\displaystyle C\) бұрышы \(\displaystyle 58^{\circ}{\small }\)- қа тең, \(\displaystyle AD\) және \(\displaystyle BE\)– \(\displaystyle O{\small }\) нүктесінде қиылысатын биссектриса
Бұрышты \(\displaystyle AOB{\small }\) табыңыз
Егер \(\displaystyle \angle A=x{\small , } \) ал \(\displaystyle \angle B=y{\small .} \) Сонымен үшбұрыштағы бұрыштардың қосындысы \(\displaystyle 180^\circ{\small , } \) тең, онда
\(\displaystyle \angle A+ \angle B+ \angle C= 180^\circ{\small , } \)
яғни \(\displaystyle x+y+58^\circ= 180^\circ{\small .} \)
Бұрыш \(\displaystyle OAB \) бұрышының жартысына тең \(\displaystyle A{\small , } \) яғни \(\displaystyle \angle OAB= \frac{ x}{ 2}{\small .} \)
Бұрыш \(\displaystyle OBA \) бұрышының жартысына тең \(\displaystyle B{\small , } \) яғни \(\displaystyle \angle OBA= \frac{ y}{ 2}{\small .} \)
Онда
\(\displaystyle x+y= 180^\circ-58^\circ{\small ,} \)
\(\displaystyle x+y= 122^\circ, \)
Демек, \(\displaystyle \frac{ x}{ 2}+ \frac{y}{2}= 61^\circ{\small . } \)
\(\displaystyle \angle OAB+ \angle OBA+ \angle AOB= 180^\circ{\small , } \)
\(\displaystyle \frac{ x}{ 2}+ \frac{y}{2}+\angle AOB= 180^\circ{\small , } \)
\(\displaystyle 61^\circ+ \angle AOB= 180^\circ{\small , } \)
\(\displaystyle \angle AOB= 180^\circ- 61^\circ= 119^\circ{\small . } \)
Жауап: \(\displaystyle 119 {\small . } \)