\(\displaystyle ABC \) үшбұрышында \(\displaystyle \angle A\) бұрышы \(\displaystyle 40^{\circ}{\small }\) тең. \(\displaystyle B \) бұрышының сыртқы бұрышы \(\displaystyle 102^{\circ}.\) \(\displaystyle C{\small }\) бұрышын табыңыз.
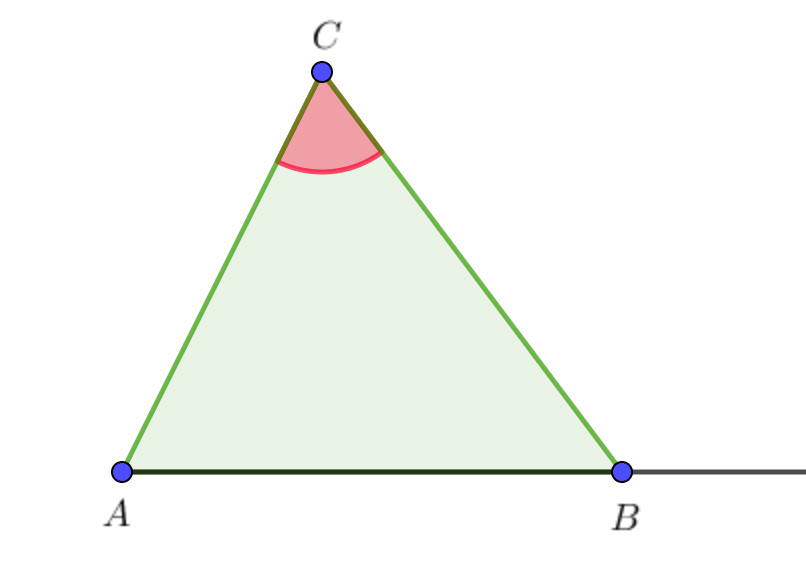
Төбедегі сыртқы бұрыш оған іргелес емес ішкі бұрыштардың қосындысына тең болғандықтан, онда \(\displaystyle \angle A+ \angle C=102^{\circ}{\small .} \) Демек,
\(\displaystyle 40+ \angle C=102{\small , } \)
\(\displaystyle \angle C=102-40{\small , } \)
\(\displaystyle \angle C=62{\small .} \)
Жауап: \(\displaystyle 62 {\small .} \)