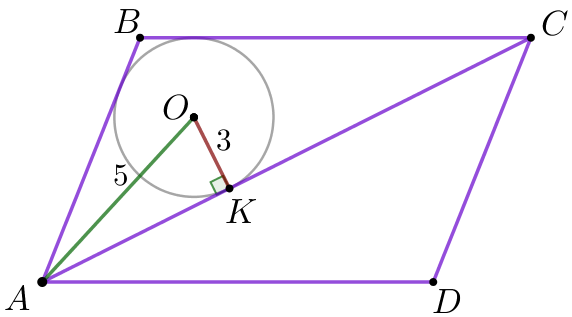
\(\displaystyle ABCD\) параллелограммында \(\displaystyle AC {\small}\) диагоналы жүргізілді \(\displaystyle O\) нүктесі \(\displaystyle ABC {\small}\) үшбұрышына іштей сызылған шеңбердің центрі болып табылады \(\displaystyle O\) нүктесінен \(\displaystyle A\) нүктесіне және \(\displaystyle AC\) түзуіне дейінгі қашықтық сәйкесінше \(\displaystyle 5\) және \(\displaystyle 3{\small}\) тең. Егер \(\displaystyle ABCD \) параллелограммының ауданы \(\displaystyle 168 \) тең болса, \(\displaystyle BC \) қабырғасының ұзындығын табыңыз
Есептің шарты бойынша сызбаны орындаймыз.
\(\displaystyle ABCD\) – параллелограмм, \(\displaystyle AC\) – параллелограммның диагоналы болсын,
\(\displaystyle O\)– \(\displaystyle ABC {\small}\) үшбұрышына іштей сызылған шеңбердің центрі
 |
|
\(\displaystyle BC{\small}\) қабырғасының ұзындығын табу қажет
\(\displaystyle M\) және \(\displaystyle N\) – әріптерімен сәйкесінше \(\displaystyle AB\) және \(\displaystyle BC\) қабырғаларымен шеңбердің жанасу нүктелерін белгілейік. \(\displaystyle OM {\small,}\) \(\displaystyle ON\) және \(\displaystyle OK\) кесінділері іштей сызылған шеңбердің радиусы сияқты тең. Яғни \(\displaystyle OM=ON=OK=3 {\small.}\) \(\displaystyle BN=x {\small,}\) \(\displaystyle CN=y {\small}\) болсын. Сонда \(\displaystyle BC=x+y{\small.}\) | 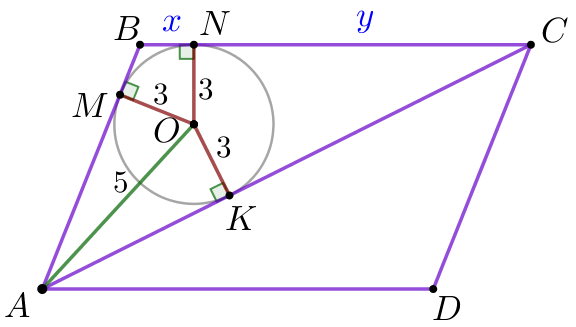 |
\(\displaystyle AC\) диагоналы \(\displaystyle ABCD\) параллелограммын екі тең үшбұрышқа бөледі:
\(\displaystyle \triangle ABC= \triangle ADC\) (үш жағы бойынша).
Демек,
\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot S_{ABCD} {\small;}\)
\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot 168=84 {\small.}\)
\(\displaystyle ABC{\small}\) үшбұрышын қарастырайық
Бір нүктеден жүргізілген шеңберге жанама кесінділер тең болғандықтан, онда
\(\displaystyle BN=BM=x {\small,}\) \(\displaystyle CN=CK=y \) және \(\displaystyle AM=AK{\small.}\)
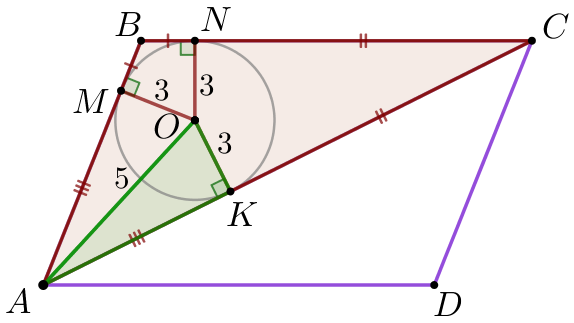 | Пифагор теоремасы бойынша \(\displaystyle AOK\) тікбұрышты үшбұрышынан \(\displaystyle AK\) кесіндісінің ұзындығын табамыз: \(\displaystyle AK^2=AO^2-OK^2 {\small;}\) \(\displaystyle AK^2=5^2-3^2 =25-9=16=4^2{\small.}\) Кесіндінің ұзындығы теріс болуы мүмкін емес болғандықтан, онда \(\displaystyle AK=4{\small.}\) |
\(\displaystyle \triangle ABC {\small}\) қабырғаларының ұзындығын жазайық \(\displaystyle BC=x+y{\small,}\) \(\displaystyle AB=x+4{\small,}\) \(\displaystyle AC=y+4{\small.}\) Үшбұрыштың периметрі барлық қабырғалардың ұзындықтарының қосындысына тең: \(\displaystyle P_{\triangle ABC}=BC+AB+AC{\small;}\) \(\displaystyle P_{\triangle ABC}=x+y+x+4+y+4=2 \cdot (x+y+4){\small.}\) | 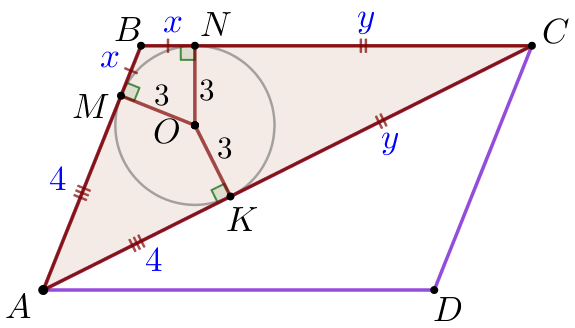 |
\(\displaystyle x+y=BC{\small}\) ескере отырып, төмендегіні аламыз
\(\displaystyle P_{\triangle ABC}=2 \cdot (BC+4){\small.}\)
Іштей сызылған шеңбердің периметрі мен радиусы арқылы үшбұрыштың ауданын өрнектейік:
\(\displaystyle S_{\triangle ABC}=\frac{1}{2} \cdot P_{\triangle ABC} \cdot r{\small;}\)
\(\displaystyle r=OK=3{\small;}\)
\(\displaystyle S_{\triangle ABC}=\frac{1}{\cancel{2}} \cdot \cancel{2} \cdot (BC+4) \cdot 3=3\cdot BC+12{\small.}\)
Себебі
\(\displaystyle S_{\triangle ABC}=84\) және \(\displaystyle S_{\triangle ABC}=3\cdot BC+12{\small,}\)
онда
\(\displaystyle 84=3\cdot BC+12{\small;}\)
\(\displaystyle 3\cdot BC=72 {\small;}\)
\(\displaystyle BC=24 {\small.}\)
Жауабы: \(\displaystyle 24{\small.}\)