Периметрі \(\displaystyle 100{\small,}\) тең және ауданы \(\displaystyle 500 {\small}\) тең болатын теңбүйірлі трапецияға шеңберді іштей сызуға болады. Трапеция табандарының ұзындығын табыңыз.
Трапецияның кіші табаны \(\displaystyle ;\)
Трапецияның үлкен табаны \(\displaystyle .\)
Тапсырманың шарты бойынша сызба саламыз.
\(\displaystyle ABCD\) – шеңбер іштей сызылған теңбүйірлі трапеция болсын, бұл ретте:
 |
Шарт бойынша:
|
Трапеция табандарының ұзындығын табу қажет.
Алдымен трапецияның бүйір жағы мен биіктігін табамыз.
Есептің шарты бойынша теңбүйірлі трапецияға шеңбер іштей сызылған.
\(\displaystyle AD+BC=AB+CD {\small.}\)
Трапеция периметрі – бұл трапецияның барлық қабырғаларының ұзындықтарының қосындысы.
\(\displaystyle P_{ABCD}=AD+BC+AB+CD {\small.}\)
Демек, табандарының қосындысы мен бүйір жақтарының қосындысы периметрдің жартысына тең:
\(\displaystyle AD+BC=AB+CD=\frac{1}{2} \cdot P_{ABCD}=\frac{1}{2}\cdot 100=50{\small.}\)
\(\displaystyle (AB=CD) {\small}\) трапеция теңбүйірлі болғандықтан, онда
\(\displaystyle AB+CD =2 \cdot AB {\small.}\)
Төмендегіні аламыз
\(\displaystyle AD+BC=2\cdot AB=50{\small;}\\ \)
\(\displaystyle \frac{AD+BC}{2}=AB=25{\small.} \)
Әрі қарай трапецияның биіктігін табамыз.
\(\displaystyle B\) нүктесінен \(\displaystyle AD\) табанына \(\displaystyle BH{\small}\) перпендикулярын жүргізейік \(\displaystyle BH\)– \(\displaystyle ABCD{\small}\) трапециясының биіктігі
| 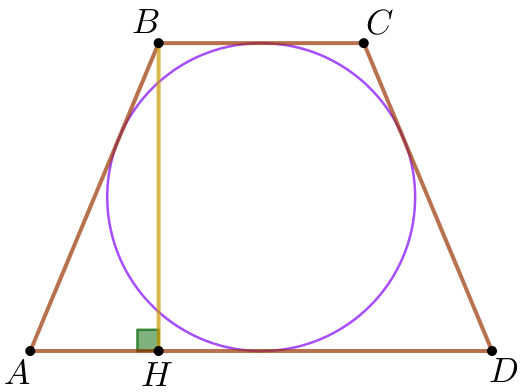 |
Трапеция ауданының формуласын қолданайық.
Трапеция ауданы
Трапеция ауданы биіктікке табандардың жарты қосындысының көбейтіндісіне тең.
| \(\displaystyle S=\frac{\color{blue}{a}+\color{blue}{b}}{2}\cdot \color{red}{h}\) |
Төмендегіні аламыз
\(\displaystyle S_{ABCD}= \frac{AD+BC}{2} \cdot BH{\small.}\\ \)
Аудан формуласына \(\displaystyle (S_{ABCD}=500{\small,} \) \(\displaystyle \frac{AD+BC}{2}=25) \) белгілі мәндерін алмастырып қоямыз және \(\displaystyle BH{\small}\\ \) табамыз
\(\displaystyle 500=25 \cdot BH{\small,}\)
\(\displaystyle BH=20{\small.}\)
\(\displaystyle BC\) және \(\displaystyle AD{\small}\) табандарын табайық
Қосымша сызбаны орындайық.
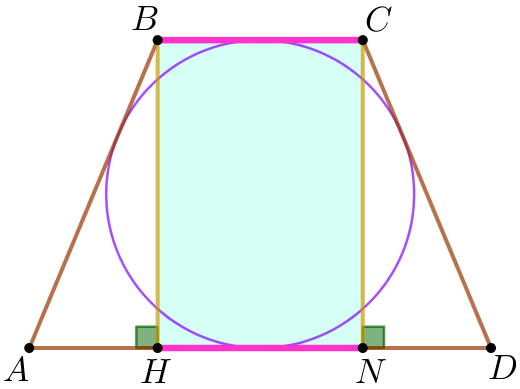 | \(\displaystyle C\) төбесінен \(\displaystyle AD\) табанына \(\displaystyle CN {\small}\) перпендикулярын жүргізейік \(\displaystyle BH=CN=20\) – трапеция биіктігі. \(\displaystyle BCNH\) – тіктөртбұрыш. Яғни, \(\displaystyle HN=BC {\small.}\) Сонда \(\displaystyle AD=AH+BC+DN {\small.}\) |
\(\displaystyle ABH\) және \(\displaystyle DCN {\small}\) тіктөртбұрышты үшбұрыштарды қарастырайық
Яғни,\(\displaystyle \triangle ABH= \triangle DCN\) (гипотенуза және катет бойынша). Демек, \(\displaystyle AH=DN {\small.}\) | 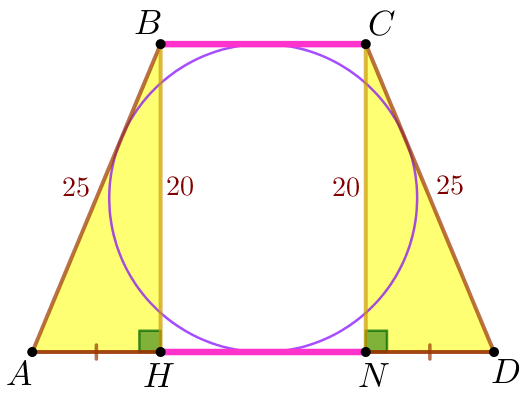 |
Пифагор теоремасы бойынша \(\displaystyle ABH\) үшбұрышынан
\(\displaystyle AH^2=AB^2-BH^2 {\small;}\)
\(\displaystyle AH^2=25^2-20^2=625-400=225=15^2 {\small.}\)
Кесіндінің ұзындығы теріс болуы мүмкін емес болғандықтан, онда \(\displaystyle AH=15 {\small.}\)
Төмендегіні аламыз
\(\displaystyle AD=AH+BC+DN {\small;}\)
\(\displaystyle AD=15+BC+15=BC+30{\small.}\)
Табандарының қосындысын біле отырып \(\displaystyle BC\) және \(\displaystyle AD{\small}\) табандарының ұзындығын табамыз
\(\displaystyle AD+BC=50 {\small;}\)
\(\displaystyle BC+30+BC=50 {\small;}\)
\(\displaystyle 2 \cdot BC=20 {\small;}\)
\(\displaystyle BC=10{\small;}\)
\(\displaystyle AD=50-BC=50-10=40{\small.}\)
Жауабы: \(\displaystyle BC=10{\small;}\) \(\displaystyle AD=40{\small.}\)