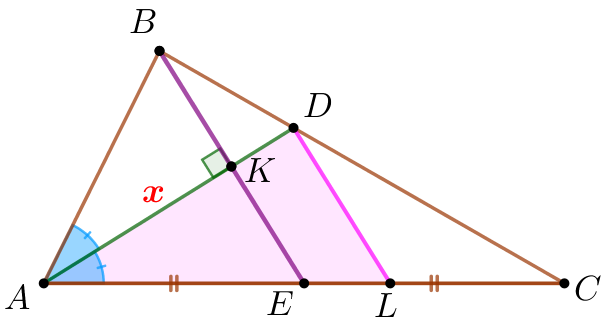
\(\displaystyle ABC \) үшбұрышында \(\displaystyle BE \) биссектрисасы мен \(\displaystyle AD \) медианасы перпендикуляр және \(\displaystyle K \) нүктесінде қиылысады. \(\displaystyle AK \) кесіндісінің ұзындығын табыңыз, егер \(\displaystyle AD=12 \) болса
Есептің шарты бойынша сызбаны орындаймыз.
 |
\(\displaystyle AE=EC {\small.}\)
\(\displaystyle \angle BAD=\angle CAD {\small.}\)
|
\(\displaystyle AK{\small}\) кесіндінің ұзындығын табу қажет
\(\displaystyle AK=x {\small}\) болсын, сонда \(\displaystyle KD=12-x {\small.}\)
Қосымша сызбаны орындайық..
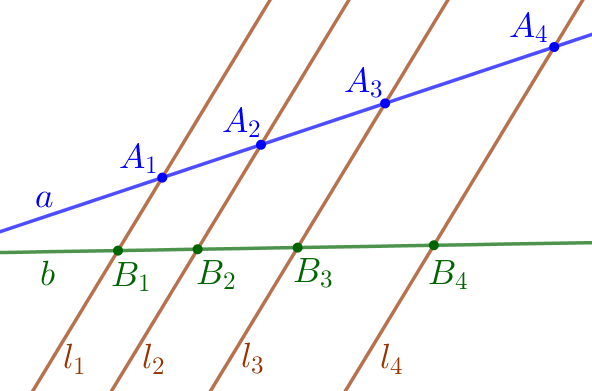
 | \(\displaystyle BE{\small}\) медианасына параллель \(\displaystyle DL\) кесіндісін салайық |
төмендегіні аламыз:
\(\displaystyle \frac{AK}{KD}= \frac{AE}{EL} {\small;}\\ \)
\(\displaystyle \frac{x}{12-x}= \frac{AE}{EL} {\small.}\)
\(\displaystyle AE=EC=a {\small}\) болсын. Сонда
\(\displaystyle \frac{x}{12-x}= \frac{a}{EL} {\small.}\)
\(\displaystyle a {\small}\) арқылы \(\displaystyle EL\) өрнектейік
\(\displaystyle BCE{\small}\) үшбұрышын қарастырайық
 | Құрылымы бойынша \(\displaystyle DL \parallel BE {\small.}\) Жалпыланған Фалес теоремасы бойынша төмендегіні аламыз: \(\displaystyle \frac{EL}{LC}=\frac{BD}{DC}{\small.}\) |
Есептің шарты бойынша \(\displaystyle AD\) – \(\displaystyle ABC{\small}\) үшбұрышының биссектрисасы
төмендегіні аламыз:
\(\displaystyle \frac{BD}{DC}=\frac{AB}{AC}{\small.} \)
Демек,
\(\displaystyle \frac{EL}{LC}=\frac{AB}{AC}{\small.}\)
\(\displaystyle ABE {\small}\) үшбұрышын қарастырайық
\(\displaystyle AK\) биссектрисасы \(\displaystyle ABE {\small}\) үшбұрышының биіктігі болғандықтан, онда \(\displaystyle \triangle ABE \) – теңбүйірлі болады.
Демек , \(\displaystyle AB=AE=a {\small.}\) Себебі \(\displaystyle AC=AE+EC \) және \(\displaystyle AE=EC=a {\small,}\) болғандықтан, онда \(\displaystyle AC=2 \cdot a{\small.}\) | 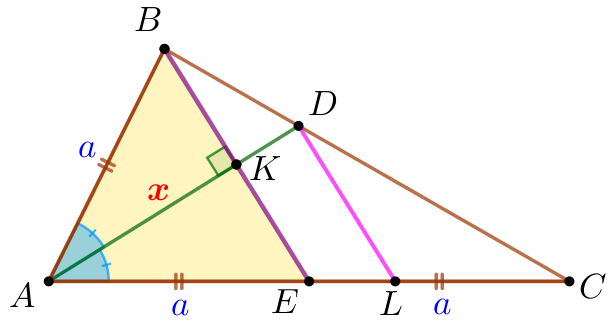 |
Төмендегіні аламыз:
\(\displaystyle \frac{EL}{LC}=\frac{AB}{AC}= \frac{a}{2 \cdot a}=\frac{1}{2}{\small.}\\ \)
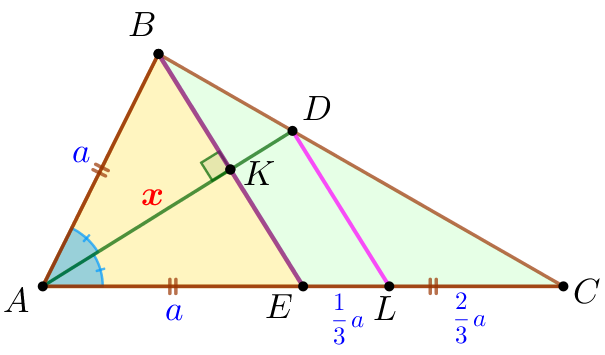 | Яғни \(\displaystyle LC=2 \cdot EL {\small.}\) Сурет бойынша \(\displaystyle EC=EL+LC {\small}\) Сонда \(\displaystyle a=EL+ 2 \cdot EL=3 \cdot EL{\small.}\) Демек, \(\displaystyle EL= \frac{1}{3} \cdot a {\small.}\) |
Себебі
\(\displaystyle \frac{x}{12-x}= \frac{a}{EL} \) және \(\displaystyle \frac{a}{EL}=\frac{\cancel{a}}{\frac{1}{3} \cdot \cancel{a}}=3 {\small}\) болғандықтан,
онда
\(\displaystyle \frac{x}{12-x}= 3 {\small.}\)
Төмендегіні аламыз
\(\displaystyle x=3 \cdot (12-x) {\small;}\)
\(\displaystyle x=36-3x {\small;}\)
\(\displaystyle 4 \cdot x=36 {\small;}\)
\(\displaystyle x=9 {\small.}\)
Демек, \(\displaystyle AK=9 {\small.}\)
Жауабы: \(\displaystyle 9 {\small.}\)