Үшбұрыштың төбелері оған сырттай сызылған шеңберді ұзындығы \(\displaystyle 6:7:23\) болатын үш доғаға бөледі. Үшбұрыштың кіші бұрышын табыңыз.
\(\displaystyle ABC\) – шеңберге іштей сызылған үшбұрыш болсын. Бұл ретте
\(\displaystyle \overset{\smile}{AB}:\overset{\smile}{BC}:\overset{\smile}{AC}=6:7:23 {\small.} \)
Үшбұрыштың төбелері оған сырттай сызылған шеңберді бөлетін доғалардың градустық өлшемдерін табамыз.
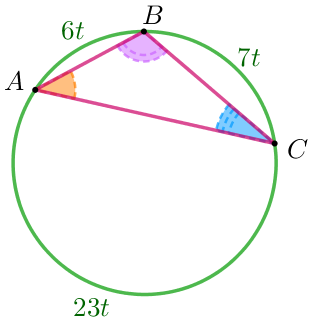 | \(\displaystyle \overset{\smile}{AB}=6t {\small,}\) \(\displaystyle \overset{\smile}{BC}=7t {\small,}\) \(\displaystyle \overset{\smile}{AC}=23t {\small}\) белгілейік Шеңбердің градустық өлшемі \(\displaystyle 360^{\circ} {\small,}\) тең болғандықтан, онда \(\displaystyle \overset{\smile}{AB}+\overset{\smile}{BC}+\overset{\smile}{AC}=360^{\circ} {\small.} \) Төмендегіні аламыз \(\displaystyle 6t+7t+23t=360^{\circ} {\small,}\) \(\displaystyle 36t=360^{\circ} {\small,}\) \(\displaystyle t=10^{\circ} {\small.}\) |
Демек,
\(\displaystyle \overset{\smile}{AB}=60^{\circ} {\small,}\) \(\displaystyle \overset{\smile}{BC}=70^{\circ} {\small,}\) \(\displaystyle \overset{\smile}{AC}=230^{\circ} {\small.}\)
Іштей сызылған бұрыш ол тірелетін доғаның жартысымен өлшенеді.
\(\displaystyle ABC {\small}\) үшбұрышы бұрыштарының градустық өлшемдерін табайық
\(\displaystyle \angle A = \frac{1}{2}\cdot \overset{\smile}{BC}=\frac{1}{2} \cdot 70^{\circ} =35^{\circ}{\small,} \\ \)
\(\displaystyle \angle B = \frac{1}{2}\cdot \overset{\smile}{AC}=\frac{1}{2} \cdot 230^{\circ}=115^{\circ}{\small,} \\ \)
\(\displaystyle \angle C = \frac{1}{2}\cdot \overset{\smile}{AB}=\frac{1}{2} \cdot 60^{\circ} =30^{\circ}{\small.} \)
\(\displaystyle \angle C =30^{\circ}\) – \(\displaystyle ABC{\small}\) үшбұрышының кіші бұрышы
Жауабы: \(\displaystyle 30 {\small.}\)