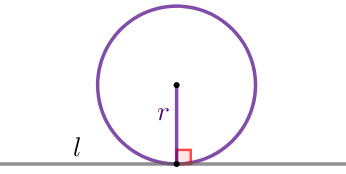
\(\displaystyle ABC\) үшбұрышының \(\displaystyle AC\) қабырғасында центрі бар шеңбер \(\displaystyle C\) төбесі арқылы өтеді және \(\displaystyle B \) нүктесінде \(\displaystyle AB\) түзуін жанайды . Егер шеңбердің диаметрі \(\displaystyle 16 ,\) aл \(\displaystyle AB=15 \) тең болса, \(\displaystyle AC\) табыңыз.
Есептің шарты бойынша сызба салайық.
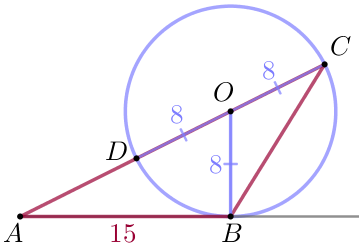 | \(\displaystyle O\) нүктесі \(\displaystyle ABC\) үшбұрышының \(\displaystyle AC {\small}\) қабырғасында жатыр \(\displaystyle O\) нүктесінде центрі бар шеңбер берілген үшбұрыштың \(\displaystyle C\) және \(\displaystyle B\) төбелері арқылы өтеді \(\displaystyle D\) әрпімен осы шеңбер \(\displaystyle AC {\small}\) қабырғасын қиып өтетін нүктені белгілейік . \(\displaystyle CD=16\) – шеңбердің диаметрі, \(\displaystyle AB=15 {\small.}\) \(\displaystyle OD=OC=OB=\frac{1}{2} \cdot 16=8 \) – шеңбер радиусы. |
1-шешу тәсілі
\(\displaystyle AOB {\small}\) үшбұрышын қарастырайық
Пифагор теоремасы бойынша \(\displaystyle AO^2=AB^2+OB^2 {\small,}\) \(\displaystyle AO^2=15^2+8^2 {\small,}\) \(\displaystyle AO^2=225+64=289=17^2 {\small.}\) Кесіндінің ұзындығы теріс болуы мүмкін емес болғандықтан, онда \(\displaystyle AO=17{\small.}\) | 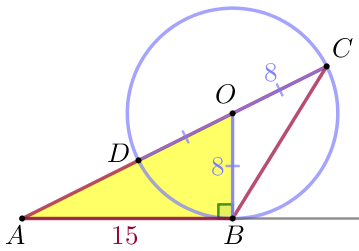 |
\(\displaystyle AC\) кесіндісінің ұзындығы \(\displaystyle AO\) және \(\displaystyle OC {\small}\) кесінділерінің ұзындығының қосындысына тең:
\(\displaystyle AC=AO+OC {\small,}\)
\(\displaystyle AC=17+8=25{\small.}\)
Жауабы: \(\displaystyle 25 {\small.}\)
2-шешу тәсілі
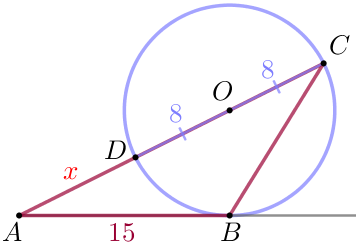 | \(\displaystyle AB^2=AC \cdot AD {\small,}\) мұндағы:
|
Алмастыра отырып, төмендегіні аламыз:
\(\displaystyle 15^2=(x+16) \cdot x {\small,}\)
\(\displaystyle 225=x^2+16x {\small,}\)
\(\displaystyle x^2+16x-225=0{\small.}\)
Кесіндінің ұзындығы теріс болуы мүмкін емес болғандықтан, онда \(\displaystyle x=9{\small.}\)
Сонда
\(\displaystyle AC=x+16=9+16=25 {\small.}\)
Жауабы: \(\displaystyle 25 {\small.}\)