\(\displaystyle H\) нүктесі тікбұрышты \(\displaystyle ABC \) үшбұрышының \(\displaystyle B\) тік бұрышының төбесінен жүргізілген \(\displaystyle BH\) биіктігінің табаны болып табылады. Диаметрі \(\displaystyle BH\) болатын шеңбер \(\displaystyle AB\) және \(\displaystyle CB\) қабырғаларын сәйкесінше \(\displaystyle P\) және \(\displaystyle K\) нүктелерінде қиып өтеді. Егер \(\displaystyle PK=11 \) болса \(\displaystyle BH\) табыңыз.
Есептің шарты бойынша сызба салайық.
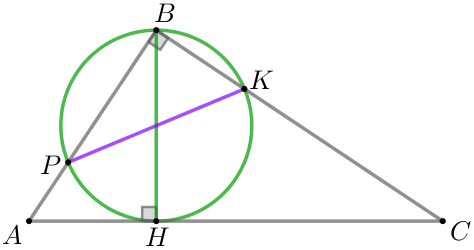 | \(\displaystyle ABC\) үшбұрышында \(\displaystyle \angle B=90^{\circ} {\small,}\) \(\displaystyle BH\) – биіктігі. Шарт бойынша \(\displaystyle BH\) – шеңбердің диаметрі. \(\displaystyle P\) және \(\displaystyle K\) нүктелері шеңберде жатыр және \(\displaystyle PK=\color{darkviolet}{11} {\small.}\) |
Салынған сызба бойынша:
- \(\displaystyle \angle PBK\) – диаметрі \(\displaystyle BH {\small}\) болатын шеңберге іштей сызылған
- \(\displaystyle \angle PBK=90^{\circ}{\small.}\)
Іштей сызылған бұрыштың шамасы
Іштей сызылған бұрыштың шамасы өзі тірелген доғаның жартысына тең.
Яғни,
\(\displaystyle \overset {\smile} {PHK}=2 \cdot \angle PBK=2 \cdot 90^{\circ}=180^{\circ} {\small.} \)
Демек, \(\displaystyle PK\) – шеңбердің диаметрі. Яғни
\(\displaystyle BH=PK=11 {\small.}\)
Жауабы: \(\displaystyle 11 {\small.}\)